Evidential Deep Learning to Quantify Classification Uncertainty 论文

Evidential Deep Learning to Quantify Classification Uncertainty 论文

论文链接: https://arxiv.org/abs/1806.01768

摘要

传统的神经网络训练目标是“最小化预测误差”，但不会告诉我们“预测的置信度”；比如模型说一张图片是猫，但它不知道自己是 80% 确定，还是只是“随便猜的”。 贝叶斯神经网络（BNN） 通过对网络权重做概率建模，间接得到预测的不确定性；但是 BNN 训练和推理代价很高，且复杂。

本文用 主观逻辑（subjective logic） 理论来建模不确定性；将分类任务中的概率分布建模为 Dirichlet 分布（而不是单一的 softmax 向量），神经网络学习到的是“收集证据的函数”，输出 Dirichlet 分布的参数。

贡献：提出一种新损失函数，驱动网络学会合理的不确定性；在分布外检测（OOD detection）和对抗攻击防御上效果突出。

简单说：他们把预测值变成了一个分布，而不是一个点数，这样网络能自然地表达“我不确定”的情况。

引言

近年来深度学习成功应用在各种任务上，性能甚至超过人类，但仍存在四大隐忧：鲁棒性、样本效率、安全性、可解释性；未来的挑战不在于“精度再提升一点点”，而是：模型能否识别“没见过的分布”？ 能否承认“我不知道”？ 能否抵御对抗攻击？

贝叶斯神经网络通过建模权重的后验分布来估计预测的不确定性，这虽然有助于模型选择、防止过拟合，但缺点是训练复杂、计算代价大。

本文用 证据理论（Theory of Evidence） 的视角来做不确定性建模；将 softmax（单一概率分布）提升为 Dirichlet 分布（分布的分布）。 直观上：

• softmax = “只给一个猜测”。

• Dirichlet = “给出一堆可能的猜测的分布”。

新的损失函数驱动网络输出 Dirichlet 参数。

前置知识

使用 Softmax 建模类别概率的缺陷

当前深度神经网络分类的主流做法是：在输出层使用 softmax 将连续激活值压缩为类别概率。

• 对于 $K$ 类问题，观测样本 $(x,y)$ 的似然函数为：

$$Pr(y|x,\theta )=Mult(y\mid \sigma (f_1(x,\theta )),\dots ,\sigma (f_K(x,\theta )))$$

其中 $Mult$ 是多项分布，$f_j(x,\theta )$ 是神经网络的第 $j$ 个输出通道，$\sigma$ 是 softmax。

• 最终训练目标是最大化 softmax 似然函数，等价于最小化交叉熵损失：

$$-\log p(y|x,\theta )=-\log \sigma (f_y(x,\theta ))$$

交叉熵的概率学解释仅是 最大似然估计 (MLE)。MLE 作为频率学派的方法，无法推断预测分布的方差。

---

Softmax 的固有问题：

• 由于指数运算，softmax 往往会夸大预测类别的概率。

• 预测结果的置信度并不可靠，新样本的“距离”只反映了与其他类别的比较，而无法衡量其绝对可靠性。

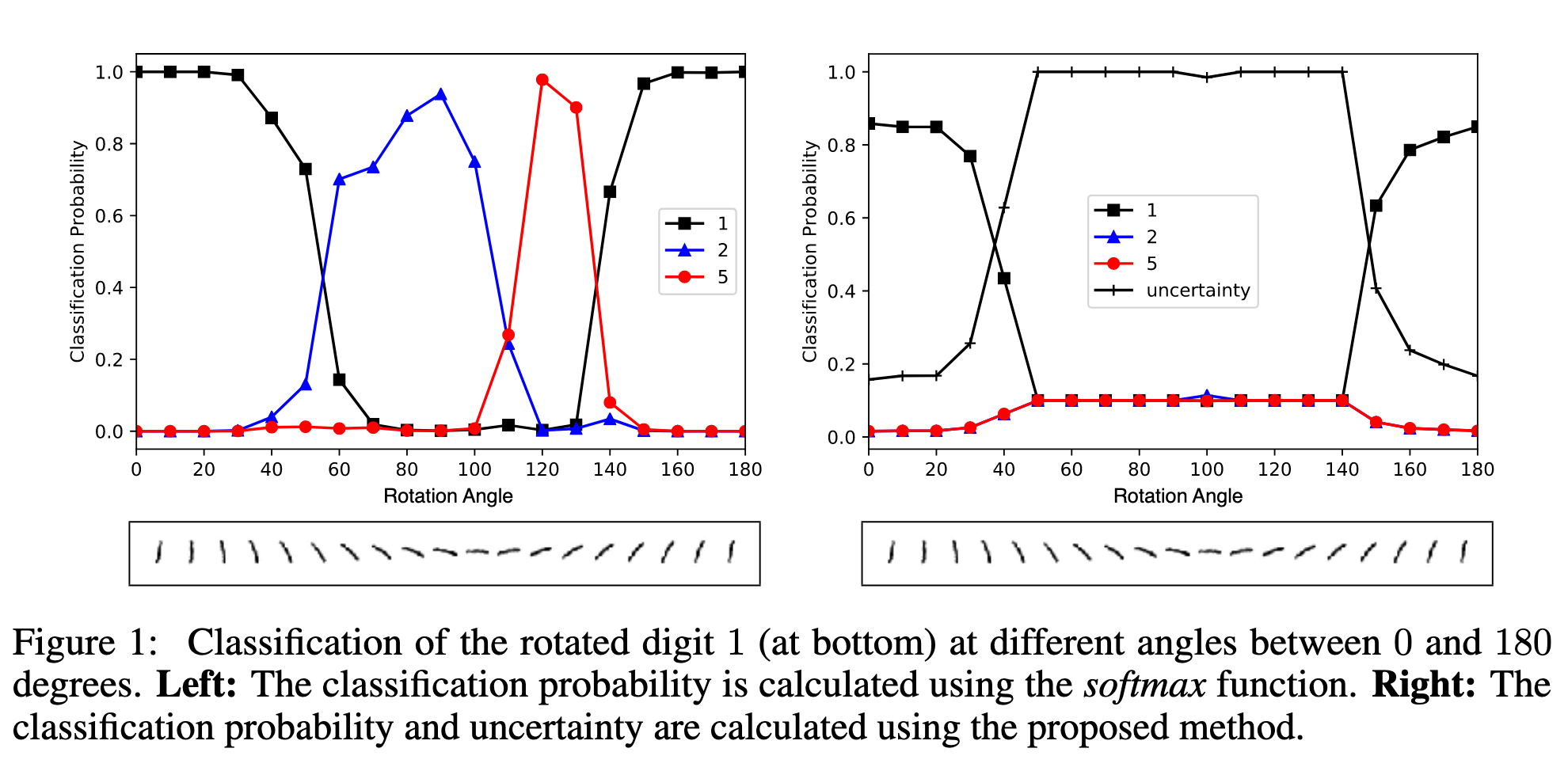
实验例子（见图1左侧）：

在 MNIST 数据集上，LeNet 对数字 1 进行分类。当图像不断逆时针旋转时，LeNet 的 softmax 输出出现错误：

• 小角度旋转时，仍能以高概率正确预测为 1。

• 当旋转角度在 ${60}^{\circ }\sim {100}^{\circ }$ 时，预测错误为数字 2。

• 当旋转角度在 ${110}^{\circ }\sim {130}^{\circ }$ 时，预测错误为数字 5。

• 错误预测时 softmax 置信度依然很高。

相比之下，本文提出的方法（见图1右侧）能够正确量化预测不确定性。

不确定性与证据理论

Dempster–Shafer 证据理论（DST） 是贝叶斯理论的推广，用来描述 主观概率。

• 它给判别框架（所有可能类别的集合）中的 子集 分配信念质量（belief mass）。

• 如果信念质量全部分配给整个集合，就相当于说 “我不知道”。

主观逻辑（SL） 将 DST 的信念分配形式化为 Dirichlet 分布，从而在严谨的框架下量化信念和不确定性。

对于 $K$ 类分类：

• 每个类别 $k$ 的信念质量为 $b_k$

• 整体不确定性质量为 $u$

它们满足：

$$u+\sum _{k=1}^K{b}_k=1,u\ge 0,b_k\ge 0$$

信念质量来源于证据 $e_k\ge 0$：

$$b_k=\frac{e_k}{S},u=\frac{K}{S}$$

其中 $S=\sum _{i=1}^K(e_i+1)$。

含义：证据总量越大，不确定性越低；没有证据时，$u=1$。

---

证据与 Dirichlet 分布：

• 信念质量分配（主观看法）对应一个 Dirichlet 分布，其参数为：

$${\alpha }_k=e_k+1$$

于是：

$$b_k=\frac{{\alpha }_k-1}{S},S=\sum _{i=1}^K{\alpha }_i$$

其中 $S$ 称为 Dirichlet 强度（strength）。

• 普通神经网络输出的是一个概率分布，而 Dirichlet 分布输出的是这些概率分布的 密度函数，因此建模了 二阶概率和不确定性。

Dirichlet 分布定义为：

$$D(p|\alpha )=\frac{1}{B(\alpha )}\prod _{i=1}^K{p}_i^{{\alpha }_i-1},p\in S_K$$

其中 $S_K=p\mid \sum _{i=1}^K{p}_i=1,0\le p_i\le 1$，$B(\alpha )$ 是多项 Beta 函数。

---

例子：10 类问题

• 如果 $b=⟨0,\dots ,0⟩$，表示没有证据。此时对应均匀分布 $D(p|⟨1,\dots ,1⟩)$，意味着完全不确定 $u=1$。

• 如果 $b=⟨0.8,0,\dots ,0⟩$，则信念为 0.8，不确定性为 0.2。由于 $K=10$，强度 $S=10/0.2=50$，类别1的证据量为 $50\times 0.8=40$。对应分布为：

$$D(p|⟨41,1,\dots ,1⟩)$$

在这种情况下，类别 $k$ 的期望概率为：

$${\hat{p}}_k=\frac{{\alpha }_k}{S}$$

当观察到新样本特征支持某类别时，相应的 ${\alpha }_j$ 会增加，表示证据积累。

---

本文观点：

神经网络不仅能输出类别概率，还能输出 Dirichlet 分布，即形成“主观看法”。

• 对于样本 $i$，若其 Dirichlet 参数为 ${\alpha }_i=⟨{\alpha }_{i1},\dots ,{\alpha }_{iK}⟩$，则 $({\alpha }_{ij}-1)$ 表示网络对类别 $j$ 的证据量。

• 基于这些参数，可以利用公式 (1) 直接计算分类的不确定性。

学习形成主观看法（Learning to Form Opinions）

传统 softmax 只提供单点概率估计，无法表达不确定性。本文方法使用 多项意见（multinomial opinions） 或等价的 Dirichlet 分布 来建模类别概率的分布。

具体做法：

• 对样本 $i$，神经网络输出一个证据向量 $f(x_i|\mathrm{\Theta })$，其中 $\mathrm{\Theta }$ 为网络参数。

• 将证据向量转化为 Dirichlet 参数：

$${\alpha }_i=f(x_i|\mathrm{\Theta })+1$$

• Dirichlet 分布的均值 ${\alpha }_i/S_i$ 可作为类别概率的估计。

• 网络结构与传统网络类似，唯一不同是 去掉 softmax 层，改为保证非负输出的激活函数（如 ReLU），作为证据向量。

损失函数设计

Dirichlet Type II 最大似然

我们把 Dirichlet 分布 $D(p_i|{\alpha }_i)$ 当作 多项分布（Multinomial）类别概率的先验，然后把类别概率“积分掉”，得到一个针对样本的总损失。

公式

$$L_i(\mathrm{\Theta })=\sum _{j=1}^K{y}_{ij}(\log S_i-\log {\alpha }_{ij})$$

其实是在衡量 总证据量 $S_i$ 和正确类别证据量 ${\alpha }_{ij}$ 的差距。

• 如果正确类别证据占总证据比例高 → 损失小

• 如果正确类别证据占比低 → 损失大

最小化这个损失的过程，相当于在让网络学会 为正确类别生成尽可能多的证据，同时避免浪费证据在错误类别上，这就是所谓的 Type II 最大似然（Type II Maximum Likelihood）。

---

贝叶斯风险下的交叉熵损失

$$L_i(\mathrm{\Theta })=\sum _{j=1}^K{y}_{ij}(\psi (S_i)-\psi ({\alpha }_{ij}))$$

• 其中 $\psi$ 为 digamma 函数。

贝叶斯交叉熵损失理解:

1. 普通交叉熵 (One-hot 标签)

• 标签是 one-hot，比如 $y=(1,0,0,...,0)$，类别 $j$ 是正确类。

• 损失函数就是：

$$CE=-\log p_j$$

也就是直接看 正确类别的预测概率。

2. EDL (Evidential Deep Learning) 的区别

• EDL 不直接输出一个概率向量 $p$，而是输出 Dirichlet 分布的参数 $\alpha =({\alpha }_1,...,{\alpha }_K)$。

• Dirichlet 分布 $Dir(p|\alpha )$ 表示模型认为 “概率向量 $p$ 本身是个随机变量”，并且 $p$ 在整个概率单纯形上分布。

• 所以它不是给出一个点概率 $p_j$，而是给出 一个分布，表示我对概率的信心和不确定性。

什么是概率单纯形？

在 $K$ 类分类任务里，预测的概率向量 $p=(p_1,...,p_K)$ 必须满足：

• $p_j\ge 0$（每个概率非负）

• $\sum _{j=1}^K{p}_j=1$（所有类别的概率之和等于1）

这个满足条件的集合就是 $K$ 维概率单纯形 (probability simplex)。

比如：

• $K=2$ 时，单纯形就是 一条线段（从 $(1,0)$ 到 $(0,1)$）。

• $K=3$ 时，单纯形就是 一个三角形（每个点是三维概率向量 $(p_1,p_2,p_3)$，它们加起来等于1）。

• 更高维时，就是更高维空间里的“单纯形”。

Dirichlet 分布的含义 ?

普通 softmax 输出一个固定的概率向量 $p=(p_1,...,p_K)$，表示“我就认定这是预测的概率”。

但在 EDL 里，模型输出的不是一个点概率，而是一组参数 $\alpha$，它定义了一个 Dirichlet 分布：

$$p\sim Dir(\alpha )$$

这表示：概率向量 $p$ 本身是个随机变量，它会在整个概率单纯形上“分布”。

换句话说，模型不是说“$p=(0.8,0.1,0.1)$”，而是说：

“我认为 $p$ 大概在 $(0.8,0.1,0.1)$ 附近，但可能有波动，它在单纯形上的分布由 $\alpha$ 控制。”

• 普通 CE：模型给一个“固定答案”。

• EDL：模型给一个“答案的分布”，告诉你它对概率预测的 信心程度。

举个例子：

• 如果 $\alpha =(50,2,2)$，Dirichlet 分布会集中在单纯形里靠近 $(1,0,0)$ 的区域，说明“很确信是类别1”。

• 如果 $\alpha =(5,5,5)$，Dirichlet 分布几乎覆盖整个三角形，说明“模型对哪个类别都没把握”。

所以 “$p$ 在整个概率单纯形上分布” 的核心含义是：Dirichlet 分布不是给一个固定的概率点，而是定义了概率向量可能落在哪些地方，以及落到这些地方的概率大小，从而显式表达了 不确定性。

3. 损失函数在 EDL 下的意义

在 EDL 场景中，交叉熵要变成 期望交叉熵：

$$L^c(\alpha )=-{\mathbb{E}}_{p\sim Dir(\alpha )}[\log p_j]$$

它不是只取一个点概率，而是对整个 Dirichlet 分布下的 $p_j$ 进行期望。

利用 Dirichlet 的性质：

$$\mathbb{E}[\log p_j]=\psi ({\alpha }_j)-\psi ({\alpha }_0)$$

于是：

$$L^c(\alpha )=\psi ({\alpha }_0)-\psi ({\alpha }_j)$$

4. 直观理解

• 在普通 CE 下： “只要 $p_j$ 大，我就满意。”

• 在 EDL 下： “只要 Dirichlet 分布下的大多数样本 $p_j$ 都大，我才满意。”

也就是说，它要求 正确类别的概率在整个分布的平均意义上都要高。

5. 举例

• 如果 $\alpha =(50,2,2)$： Dirichlet 分布强烈集中在类别1附近，$p_1$ 大多数时候接近 1，损失小。

• 如果 $\alpha =(5,5,5)$：Dirichlet 很分散，表示“模型不确定”，那么即使 $\mathbb{E}[p_1]=1/3$，损失也会比较大。

在 one-hot 标签下，普通 CE 直接看 预测点概率 $p_j$；而在 EDL 下，损失函数看的是 正确类别在 Dirichlet 分布上的期望概率（平均对数概率），这既考虑了预测的正确性，也考虑了模型的不确定性。

---

均方误差损失

$$L_i(\mathrm{\Theta })=\sum _{j=1}^K((y_{ij}-E[p_{ij}]{)}^2+Var(p_{ij}))=\sum _{j=1}^K(y_{ij}-\hat{p}\ast ij{)}^2+\frac{\hat{p}\ast ij(1-{\hat{p}}_{ij})}{S_i+1}$$

• 损失同时考虑 预测误差（Lerr）和 Dirichlet 分布的方差（Lvar）。

• 实验表明，相比公式3和4，公式5更稳定，且避免生成过高的信念质量。

这个损失有两部分：

(1) 预测误差（Lerr）

$$(y_{ij}-{\hat{p}}_{ij}{)}^2$$

和普通回归的 MSE 很像，要求正确类别的均值概率接近 1，错误类别接近 0。

(2) 不确定性惩罚（Lvar）

$$Var(p_{ij})=\frac{\hat{p}\ast ij(1-\hat{p}\ast ij)}{S_i+1}$$

这个部分体现 模型的信心程度。

• 如果 $S_i$ 很大（模型收集到的证据很多），方差就很小，模型更确定。

• 如果 $S_i$ 很小（证据少），方差就很大，说明模型对这个样本没那么确定。

损失函数会鼓励模型在证据不足时保持较大的不确定性，而不是盲目地给出“过高的信心”。

直观理解:

• 普通 CE 或 MSE：只关心“预测均值对不对”。

• EDL 的 MSE 损失：既关心“预测均值对不对”，又关心“预测的信心是否合理”。

换句话说，模型不仅要输出正确答案，还要学会“我知道自己知道/不知道”。

举个例子:

假设是 3 分类问题，正确类别是 1。

• 情况A：$\alpha =(50,1,1)$

  • $\hat{p}=(0.96,0.02,0.02)$，$S=52$，方差小

  • 模型预测准而且很有信心，loss 低 ✅

• 情况B：$\alpha =(5,5,5)$

  • $\hat{p}=(0.33,0.33,0.33)$，$S=15$，方差大

  • 预测不准且不确定，loss 高 ❌

• 情况C：$\alpha =(1,1,1)$

  • $\hat{p}=(0.33,0.33,0.33)$，$S=3$，方差更大

  • 表示“完全没有证据”，模型保持高不确定性，此时损失比 B 稍好，因为它“知道自己不知道”。

为什么它比公式3、4更稳定？

• 公式3（对数似然损失）和公式4（贝叶斯交叉熵）在训练早期，容易导致网络输出 过高的证据量（$\alpha$ 很大），从而假装“很自信”但其实没学好。

• 公式5 加入了方差项，相当于一个正则化，避免了“虚假高信念”，让模型更稳健。

均方误差损失在 EDL 中的意义就是：不仅要求预测正确（均值对标签接近），还要求不确定性合理（方差与证据匹配），因此能避免“盲目自信”，训练更稳定。

---

损失函数的理论性质

1. Proposition 1：对于任意 ${\alpha }_{ij}\ge 1$，方差项 $L_{ij}^{var}$ 小于误差项 $L_{ij}^{err}$，保证数据拟合优先于方差最小化。

2. Proposition 2：对于正确类别 $j$，增加 ${\alpha }_{ij}$ 的证据会降低 $L_i^{err}$，删除证据会增加 $L_i^{err}$。

• 这保证网络能生成足够的证据以正确拟合训练数据。

3. Proposition 3（学习型损失衰减）：对于正确类别 $j$，减少其他类别 $l\ne j$ 的最大 Dirichlet 参数 ${\alpha }_{il}$ 的证据会降低 $Ler{r}_i$。

• 这保证网络能够自动减少误导性证据，避免错误分类。

综合三条性质：网络会 为正确类别生成更多证据，同时 删除误导性证据，并在训练集上尽量减少预测方差。

---

批量训练与模式学习

• 对一批样本的总损失为每个样本损失之和。

• 网络可发现数据模式，并生成与模式对应的证据。例如：

  • MNIST 图像中出现大圆形模式 → 生成数字 0 的证据增加。

  • 出现反例（如数字 6 的大圆形） → 网络通过反向传播减少该模式生成的证据。

• 当反例数量有限时，减少误导证据可能增加总损失，但只要正确类别证据最大，问题不大。

---

不确定性建模与 KL 正则化

• 如果样本无法正确分类，希望 总证据趋近于零，对应均匀 Dirichlet 分布（完全不确定，$u=1$）。

• 通过加入 KL 散度正则项，将预测分布与“我不知道”状态的偏离纳入损失：

$$L(\mathrm{\Theta })=\sum _{i=1}^N{L}_i(\mathrm{\Theta })+{\lambda }_t\sum _{i=1}^{N}KL[D(p_i|{\tilde{\alpha }}_i)||D(p_i|⟨1,\dots ,1⟩)]$$

• ${\lambda }_t=min(1.0,t/10)$ 随训练逐步增加，避免训练早期过早收敛到均匀分布。

• ${\tilde{\alpha }}_i=y_i+(1-y_i){\alpha }_i$，去掉非误导性证据后的 Dirichlet 参数。

• KL 散度公式：

$$KL[D(p_i|\tilde{\alpha }\ast i)||D(p_i|1)]=\log \frac{\mathrm{\Gamma }(\sum _k\tilde{\alpha }\ast ik)\mathrm{\Gamma }(K)}{\prod _k\mathrm{\Gamma }(\tilde{\alpha }\ast ik)}+\sum _k(\tilde{\alpha }\ast ik-1)[\psi (\tilde{\alpha }\ast ik)-\psi (\sum _j\tilde{\alpha }\ast ij)]$$

• 该策略保证网络能探索参数空间，并在未来 epoch 正确分类样本时，不会过早收敛到均匀分布。

相关工作

在不确定性建模方面，有两条主要研究路径：

第一类：高斯过程（GPs）

• GPs 能同时做到 预测精度高 和 不确定性度量可靠，在迁移学习 [15]、深度学习 [32] 等领域都有成功应用。

• GPs 在 主动学习 [12] 中的不确定性计算达到了最先进水平。

• 作为非参数模型，GPs 不需要假设确定性或随机参数，且其预测方差可 解析计算（closed form），同时能拟合广泛的非线性函数，因此被称为 通用预测器 [31]。

第二类：贝叶斯神经网络（BNNs）

• BNNs 通过对权重引入先验来建模参数不确定性。由于神经网络的非线性，权重的后验分布无法解析求解。

• 当前研究重点在于提升近似推断方法的可扩展性，如 变分贝叶斯（VB） [2, 6, 27, 23, 9] 和 随机梯度哈密顿蒙特卡洛（SG-HMC） [3]。

• 尽管 BNNs 预测能力很强，但其 后验预测分布 无法解析，需要通过 蒙特卡罗积分 近似，这会带来不确定性估计中的噪声。

与上述方法正交的路线

• 本文提出跳过参数后验的推断，直接 建模 Dirichlet 后验分布，并通过确定性神经网络从数据中学习超参数，从而更高效地进行不确定性建模。

结论

本文提出了一种新的分类预测分布设计方法：

• 在类别概率上放置 Dirichlet 分布，并将神经网络输出作为其参数。

• 通过 最小化 L2 范数损失下的贝叶斯风险，并加入信息论的复杂度正则项来拟合该分布。

• 最终预测器不再是 softmax 点估计，而是 类别概率的 Dirichlet 分布，能提供更丰富的不确定性刻画。

此外，本文还从 证据推理（evidential reasoning） 视角解释了预测器的行为，并将结果与 主观逻辑（subjective logic） 中的 信念质量与不确定性分解 联系起来。

实验结果表明，该方法在以下两个任务上显著优于现有方法：

• 分布外样本检测（out-of-distribution detection）

• 抗对抗扰动能力（endurance against adversarial perturbations）