概率论基础概念

概率论基础概念(用到多少，学多少 =_=)

概率空间

我们将概率空间定义为三元组 $(\mathrm{\Omega },\mathcal{F},P)$，其中：

• $\mathrm{\Omega }$ 是样本空间，表示实验中所有可能的结果组成的集合；

• $\mathcal{F}$ 是事件空间，即 $\mathrm{\Omega }$ 的所有子集的集合；

• $P$ 是概率度量，是一个从事件 $E\subseteq \mathrm{\Omega }$ 到 $[0,1]$ 区间数值的映射（即 $P:\mathcal{F}\to [0,1]$），满足某些一致性要求。

离散随机变量

最简单的情况是实验的结果是可数的。例如，掷一个三面骰子，其三个面分别标记为 “A”、“B”、“C”（为了简洁，我们用3面而不是6面）。此时：

• 样本空间为 $\mathrm{\Omega }=\{A,B,C\}$，表示所有可能的实验结果；

• 事件空间为 $\mathcal{F}=\{\mathrm{\varnothing },\{A\},\{B\},\{C\},\{A,B\},\{A,C\},\{B,C\},\{A,B,C\}\}$。

其中每一个事件就是事件空间中的一个元素。例如：

• 事件 $E_1=\{A,B\}$ 表示骰子掷出面为 A 或 B；

• 事件 $E_2=\{C\}$ 表示骰子掷出面为 C。

定义事件空间后，需要指定概率度量 $P$，即为事件空间中的每个集合赋予一个“权重”或“大小”。例如，设：

• $P[\{A\}]=\frac{2}{6}$，

• $P[\{B\}]=\frac{1}{6}$，

• $P[\{C\}]=\frac{3}{6}$。

则复合事件的概率可通过求和得到，例如：

• $P[\{A,B\}]=\frac{2}{6}+\frac{1}{6}=\frac{1}{2}$。

为简化记号，我们可以将每个样本空间中的结果映射为一个实数，这就定义了随机变量（random variable，记作 rv）：

随机变量 = 一个把“事件结果”映射为“数值”的函数，它本身不随机，随机的是它作用的输入（样本 $\omega$）。

• $X:\mathrm{\Omega }\to \mathbb{R}$，将每个结果 $\omega \in \mathrm{\Omega }$ 映射为实数 $X(\omega )$。

例如，对三面骰子设：

• $X(A)=1$，

• $X(B)=2$，

• $X(C)=3$。

再如，掷两次公平硬币，样本空间为：

• $\mathrm{\Omega }=\{{\omega }_1=(H,H),{\omega }_2=(H,T),{\omega }_3=(T,H),{\omega }_4=(T,T)\}$。

设随机变量 $X$ 表示“正面出现次数”，则：

• $X({\omega }_1)=2$，

• $X({\omega }_2)=1$，

• $X({\omega }_3)=1$，

• $X({\omega }_4)=0$。

我们将随机变量可能的取值集合称为其状态空间，记作 $X(\mathrm{\Omega })=\mathcal{X}$。给定某个状态 $a$，定义：

$$p_X(a)=P[X=a]=P[X^{-1}(a)]$$

其中 $X^{-1}(a)=\{\omega \in \mathrm{\Omega }|X(\omega )=a\}$，称为 $a$ 的原像。

你有一个随机变量 $X$，它是一个函数，从样本空间 $\mathrm{\Omega }$ 映射到实数；给定某个输出值 $a$，我们关心的是：随机变量等于这个值的概率是多少，即 $P[X=a]$。

但是：随机变量是函数，它本身不“随机”，真正随机的是实验结果 $\omega \in \mathrm{\Omega }$。所以，要知道“$X=a$”的概率是多少，其实等价于问：

• 有多少个 $\omega$ 会导致 $X(\omega )=a$，而这些 $\omega$ 的总概率是多少？

所以，我们这么定义：

• $X^{-1}(a)$：是所有让 $X(\omega )=a$ 成立的样本点集合（这就是“原像”）；
  
• 然后，$\boxed{{\displaystyle P[X=a]=P[X^{-1}(a)]}}$：就是计算这些 $\omega$ 的总概率。

实验：投两次硬币

$$\mathrm{\Omega }=\{(H,H),(H,T),(T,H),(T,T)\}$$

定义随机变量 $X$：表示正面（H）的次数

• $X(H,H)=2$

• $X(H,T)=1$

• $X(T,H)=1$

• $X(T,T)=0$

现在我们问：$\boxed{{\displaystyle P[X=1]=?}}$

这等价于找出：

• 哪些 $\omega$ 会导致 $X(\omega )=1$？

• 答案是 $X^{-1}(1)=\{(H,T),(T,H)\}$

如果每个 $\omega$ 的概率都是 $1/4$，那么：

$$P[X=1]=P[X^{-1}(1)]=P[\{(H,T),(T,H)\}]=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$$

这里，$p_X$ 称为概率质量函数（pmf，probability mass function）。继续上述例子，掷两次硬币的 pmf 为：

• $p_X(0)=P[\{(T,T)\}]=\frac{1}{4}$，

• $p_X(1)=P[\{(T,H),(H,T)\}]=\frac{2}{4}$，

• $p_X(2)=P[\{(H,H)\}]=\frac{1}{4}$。

pmf 可用柱状图表示，也可用参数化函数表示。我们称 $p_X$ 为随机变量 $X$ 的概率分布。在上下文明确的情况下，常省略下标 $X$。

随机变量 $X$ 把世界事件映射成数字；

pmf $p_X$ 把这些数字映射成它们发生的概率。

$$\omega \stackrel{X}{\to }a\stackrel{p_X}{\to }P[X=a]$$

连续随机变量

我们也可以考虑结果为连续值的实验。这种情况下，假设样本空间是实数集合的子集：$\mathrm{\Omega }\subseteq \mathbb{R}$，并定义随机变量为恒等函数 $X(\omega )=\omega$。

例如，测量某事件持续时间（单位：秒），设：

• $\mathrm{\Omega }=\{t:0\le t\le T_{\text{max}}\}$。

由于该集合是不可数的，无法像离散情形那样枚举所有子集。因此，我们需要借助Borel σ-代数（Borel sigma-field）来定义事件空间。其定义如下：

集合 $\mathcal{F}$ 是一个 σ-代数（sigma-field）当且仅当：

1. $\mathrm{\varnothing }\in \mathcal{F}$，且 $\mathrm{\Omega }\in \mathcal{F}$；

2. 若 $E\in \mathcal{F}$，则其补集 $E^c\in \mathcal{F}$；

3. 若 $E_1,E_2,\dots \in \mathcal{F}$，则 $\bigcup _{i=1}^{\mathrm{\infty }}{E}_i$ 与 $\bigcap _{i=1}^{\mathrm{\infty }}{E}_i$ 也属于 $\mathcal{F}$。

Borel σ-代数是由半开区间 $(-\mathrm{\infty },b]$ 生成的最小 σ-代数。通过这些区间的并、交和补运算，我们可以得到：

$$(a,b),[a,b],(a,b],[a,b],\{b\},-\mathrm{\infty }\le a\le b\le \mathrm{\infty }$$

当我们讨论连续型随机变量（比如测量一个时间、距离或温度）时，它的样本空间是连续的，比如：

$$\mathrm{\Omega }=[0,T_{\text{max}}]$$

在这种连续的空间里，所有可能的“事件”不是像离散情况那样简单地枚举出来的（比如 $\{H,T\}$），而可能是“无限多种可能的区间组合”。

比如我们可能想表示这些事件：

• “温度在 1 到 2 度之间” → 区间 (1, 2)

• “时间小于 5 秒” → 区间 $(0,5]$

• “温度是 3 度或 7 度” → $\{3,7\}$

• “测量值是无理数” → 这也算是一类事件！

但是问题是：我们不能对“所有”这样的集合都定义概率！

因为某些集合太“奇怪”或太“复杂”，会导致概率的定义出现矛盾或不收敛。

所以我们需要一个规则体系来规定“我们只对哪些集合定义概率” ——> 这个规则体系就是σ-代数（sigma-field）。

σ-代数是一个集合的集合（简单理解：是你允许讨论的事件的全集合），它必须满足以下三条规则（你可以把它们理解成“合理事件空间”的要求）：

1. 包含整个样本空间和空集

   • 你总得允许“什么都不发生”（空事件）
   • 也得允许“一定会发生”（整个样本空间）

2. 如果你能谈某个事件，那它的补集你也得能谈

   • 比如：“温度小于 30 度” 这个事件存在，那“温度不小于 30 度”这个事件也应该存在

3. 如果你能谈一堆事件，那它们的并集和交集也得能谈

   • 比如你能谈“温度在 (0,1)”、“温度在 (1,2)”……，那“温度在 (0,2)”这种组合你也得能谈

换句话说：σ-代数就是一种封闭的事件系统，允许你用基本事件构造更复杂事件，但不会跑出系统之外。

Borel σ-代数是专门为实数空间（$\mathbb{R}$）设计的一种 σ-代数，用来处理实数范围内的“正常”区间事件。

它的定义是：

Borel σ-代数是由所有形如 $(-\mathrm{\infty },b]$ 的区间生成的最小 σ-代数。

也就是说，它从一些基本的“区间事件”出发，通过反复地做并集、交集、补集操作，构造出你所需要的所有“常见事件”。

比如：

• $(a,b)$：开区间

• $[a,b]$：闭区间

• $[a,b)$、$(a,b]$：半开区间

• $\{c\}$：单点集

• 任意有限/可数个区间并集交集……

这些都属于 Borel σ-代数。

你可以把它理解成：我们定义概率，只在这些“结构正常的区间组合”上做，不碰那些太反直觉或病态的集合。

总结: Borel σ-代数是一种你可以安全地讨论概率的“事件集合体系”，它由一些基本区间（比如 $(-\mathrm{\infty },b]$）出发，闭包得到所有“常规可测的集合”。

在持续时间的例子中，可进一步限制事件空间只包含区间 $[a,b]$，其中 $0\le a\le b\le T_{\text{max}}$。

为定义概率度量，我们为每个 $x\in \mathrm{\Omega }$ 赋一个非负权重 $p_X(x)\ge 0$，称为概率密度函数（pdf，probability density function）。

对于事件 $E=[a,b]$，概率由积分给出：

$$P([a,b])={\int }_{E}dP={\int }_a^{b}p(x)dx$$

还可以定义累积分布函数（cdf）：

$$P_X(x)\triangleq P[X\le x]={\int }_{-\mathrm{\infty }}^x{p}_X(x^{\prime })d{x}^{\prime }$$

从中可以计算区间概率：

$$P([a,b])=P(a\le X\le b)=P_X(b)-P_X(a)$$

“概率分布”一词既可以指 pdf $p_X$，也可以指 cdf $P_X$，甚至指概率度量 $P$ 本身。

上述定义也可推广到多维空间 $\mathrm{\Omega }\subseteq {\mathbb{R}}^n$，以及函数等更复杂的样本空间。

概率公理

与事件空间相关联的概率规律，必须遵循概率公理（Kolmogorov 公理），具体如下：

1. 非负性（Non-negativity）：

   对任意事件 $E\subseteq \mathrm{\Omega }$，有

   $$P[E]\ge 0$$

2. 规范性（Normalization）：

   整个样本空间的概率为 1：

   $$P[\mathrm{\Omega }]=1$$

3. 可加性（Additivity）：

   对于任意一列两两互不相交（即互斥）的事件 $\{E_1,E_2,\dots \}$，有

   $$\begin{array}{}\text{(2.6)}& P\left[\bigcup _{i=1}^{\mathrm{\infty }}{E}_i\right]=\sum _{i=1}^{\mathrm{\infty }}P[E_i]\end{array}$$

   在有限的情况下，比如只有两个互斥事件 $E_1$ 和 $E_2$，上述公式简化为：

   $$\begin{array}{}\text{(2.7)}& P[E_1\cup E_2]=P[E_1]+P[E_2]\end{array}$$

   这个公式对应的是“事件 $E_1$ 或 $E_2$ 发生”的概率（前提是这两个事件是互斥的）。

从这些公理可以推导出一些常用结论：

补集规则（Complement Rule）：

$$\begin{array}{}\text{(2.8)}& P[E^c]=1-P[E]\end{array}$$

其中，$E^c=\mathrm{\Omega }\setminus E$ 表示事件 $E$ 的补集。

这个结论来自于：

$$P[\mathrm{\Omega }]=P[E\cup E^c]=P[E]+P[E^c]=1$$

其他可推出的结论：

• $P[E]\le 1$：可通过反证法证明

• $P[\mathrm{\varnothing }]=0$：可由补集规则推出，当 $E=\mathrm{\Omega }$ 时，$E^c=\mathrm{\varnothing }$，所以 $P[\mathrm{\varnothing }]=1-P[\mathrm{\Omega }]=0$

加法规则（Addition Rule）：

对于任意两个事件（不要求互斥），有：

$$\begin{array}{}\text{(2.9)}& P[E_1\cup E_2]=P[E_1]+P[E_2]-P[E_1\cap E_2]\end{array}$$

这个公式适用于任意两个事件，即使它们可能有重叠。

条件概率

考虑两个事件 $E_1$ 和 $E_2$。如果 $P[E_2]\ne 0$，则定义事件 $E_1$ 在 $E_2$ 已经发生的条件下的条件概率为：

$$\begin{array}{}\text{(2.10)}& P[E_1\mid E_2]\triangleq \frac{P[E_1\cap E_2]}{P[E_2]}\end{array}$$

根据这个定义，可以得到乘法法则（multiplication rule）：

$$\begin{array}{}\text{(2.11)}& P[E_1\cap E_2]=P[E_1\mid E_2]P[E_2]=P[E_2\mid E_1]P[E_1]\end{array}$$

条件概率衡量的是：在事件 $E_2$ 已经发生的前提下，事件 $E_1$ 发生的可能性有多大。

然而，如果两个事件是无关的，那么一个事件的发生不会改变另一个事件的概率。更形式化地说，若满足以下条件，则称 $E_1$ 与 $E_2$ 是独立事件（independent events）：

$$\begin{array}{}\text{(2.12)}& P[E_1\cap E_2]=P[E_1]\cdot P[E_2]\end{array}$$

若 $P[E_1]>0$ 且 $P[E_2]>0$，上式等价于：

• $P[E_1\mid E_2]=P[E_1]$，或

• $P[E_2\mid E_1]=P[E_2]$

同理，若在某个事件 $E_3$ 已知的条件下，事件 $E_1$ 与 $E_2$ 满足下式：

$$\begin{array}{}\text{(2.13)}& P[E_1\cap E_2\mid E_3]=P[E_1\mid E_3]\cdot P[E_2\mid E_3]\end{array}$$

则称 $E_1$ 和 $E_2$ 在给定 $E_3$ 的条件下是条件独立的（conditionally independent）。

全概率公式（Law of total probability）

根据条件概率的定义，还可以推导出全概率公式：

若集合 $\{A_1,A_2,\dots ,A_n\}$ 构成样本空间 $\mathrm{\Omega }$ 的一个划分（partition），那么对于任意事件 $B\subseteq \mathrm{\Omega }$，有：

$$\begin{array}{}\text{(2.14)}& P[B]=\sum _{i=1}^{n}P[B\mid A_i]\cdot P[A_i]\end{array}$$

全概率公式: 一个事件总体概率 = 在不同情形下它发生的概率 × 各种情形本身的概率，加起来。

假设我们有一个检测疾病的筛查工具，我们要问：

• 一个人检测为阳性的总体概率是多少？

我们知道：

• 人群中 1% 有病（记作 $A_1$），99% 无病（记作 $A_2$）；

• 如果有病（$A_1$），检测为阳性（$B$）的概率是 0.9（即 $P[B|A_1]=0.9$）；

• 如果没病（$A_2$），误报为阳性概率是 0.05（即 $P[B|A_2]=0.05$）；

问：一个人检测阳性的总体概率是多少？

我们把“人是否患病”作为划分事件：

• $A_1$：患病，$P[A_1]=0.01$

• $A_2$：未患病，$P[A_2]=0.99$

我们要算的事件是“检测为阳性”（$B$）：

$$P[B]=P[B|A_1]\cdot P[A_1]+P[B|A_2]\cdot P[A_2]$$$$=0.9\cdot 0.01+0.05\cdot 0.99=0.009+0.0495=\boxed{{\displaystyle 0.0585}}$$

所以，虽然你可能觉得“阳性概率应该很高”，但实际上总体阳性概率只有 5.85%，因为大多数人根本没病，而没病的人也有误报。

贝叶斯法则

根据条件概率的定义，可以推导出贝叶斯法则（Bayes’ rule），也称为贝叶斯定理（Bayes’ theorem）。对于任意两个满足 $P[E_1]>0$ 且 $P[E_2]>0$ 的事件 $E_1$ 和 $E_2$，有：

$$\begin{array}{}\text{(2.15)}& P[E_1\mid E_2]=\frac{P[E_2\mid E_1]\cdot P[E_1]}{P[E_2]}\end{array}$$

离散随机变量形式

对于一个具有 $K$ 个可能取值的离散随机变量 $X$，结合全概率公式，贝叶斯法则可以写为：

$$\begin{array}{}\text{(2.16)}& p(X=k\mid E)=\frac{p(E\mid X=k)\cdot p(X=k)}{p(E)}=\frac{p(E\mid X=k)\cdot p(X=k)}{\sum _{k^{\prime }=1}^{K}p(E\mid X=k^{\prime })\cdot p(X=k^{\prime })}\end{array}$$

其中：

• $p(X=k)$：称为先验概率（prior probability）

• $p(E\mid X=k)$：称为似然（likelihood）

• $p(X=k\mid E)$：称为后验概率（posterior probability）

• $p(E)$：为归一化常数，也叫作边缘似然（marginal likelihood）

连续随机变量形式

对于一个连续型随机变量 $X$，贝叶斯法则写作：

$$\begin{array}{}\text{(2.17)}& p(X=x\mid E)=\frac{p(E\mid X=x)\cdot p(X=x)}{p(E)}=\frac{p(E\mid X=x)\cdot p(X=x)}{\int p(E\mid X=x^{\prime })\cdot p(X=x^{\prime })d{x}^{\prime }}\end{array}$$

这就是贝叶斯法则在离散和连续两种情形下的表达方式，它提供了一种根据观测数据（事件 $E$）来更新我们对未知变量 $X$ 的信念的机制，是整个贝叶斯推断的核心。

一些常见的概率分布

在构建各种类型的模型时，我们会用到多种概率分布。以下小节总结了其中一些常见分布。

交互式可视化网站： 🔗 https://ben18785.shinyapps.io/distribution-zoo/

离散分布

本节讨论的是定义在（非负）整数子集上的一些离散型概率分布。

伯努利分布与二项分布（Bernoulli and Binomial distributions）

设 $x\in \{0,1,\dots ,N\}$，二项分布（Binomial distribution）定义为：

$$\begin{array}{}\text{(2.18)}& \text{Bin}(x\mid N,\mu )\triangleq (\genfrac{}{}{0ex}{}{N}{x}){\mu }^x(1-\mu {)}^{N-x}\end{array}$$

其中，$(\genfrac{}{}{0ex}{}{N}{x})\triangleq \frac{N!}{x!(N-x)!}$ 是从 $N$ 个元素中选出 $x$ 个的组合数（称为二项系数，读作 “N 选 x”）。

如果 $N=1$，即 $x\in \{0,1\}$，则二项分布退化为伯努利分布（Bernoulli distribution）：

$$\begin{array}{}\text{(2.19)}& \text{Ber}(x\mid \mu )=\{\begin{array}{ll}\mu & \text{如果 }x=1\\ 1-\mu & \text{如果 }x=0\end{array}\end{array}$$

其中，$\mu =\mathbb{E}[x]=p(x=1)$ 是分布的均值。

分类分布与多项分布（Categorical and Multinomial distributions）

如果变量是多值离散型的（例如 $x\in \{1,\dots ,K\}$），我们可以使用分类分布（categorical distribution）：

$$\begin{array}{}\text{(2.20)}& \text{Cat}(x\mid \mathit{\theta })\triangleq \prod _{k=1}^K{\theta }_k^{\mathbb{I}(x=k)}\end{array}$$

其中 ${\theta }_k$ 表示选择类别 $k$ 的概率，$\mathbb{I}(x=k)$ 是指示函数，表示当 $x=k$ 时取 1，否则取 0。

或者，也可以将 K 类变量 $x$ 表示成一个 独热编码（one-hot）向量，这时分类分布可以写为：

$$\begin{array}{}\text{(2.21)}& \text{Cat}(x\mid \mathit{\theta })\triangleq \prod _{k=1}^K{\theta }_k^{x_k}\end{array}$$

其中 $x_k=1$ 表示当前样本属于第 $k$ 类，其它元素为 0。

如果 $x_k$ 表示类别 $k$ 在总共 $N=\sum _{k=1}^K{x}_k$ 次试验中出现的次数，那么就得到了多项分布（multinomial distribution）：

$$\text{M}(x\mid N,\mathit{\theta })=\underset{\text{多少种方式出现这种次数组合}}{\underbrace{(\genfrac{}{}{0ex}{}{N}{x_1,\dots ,x_K})}}\cdot \underset{\text{每种方式下这个组合出现的概率}}{\underbrace{\prod _{k=1}^K{\theta }_k^{x_k}}}$$

其中，多项系数（multinomial coefficient）定义为：

$$\begin{array}{}\text{(2.23)}& (\genfrac{}{}{0ex}{}{N}{k_1,\dots ,k_m})\triangleq \frac{N!}{k_1!\cdots k_m!}\end{array}$$

泊松分布（Poisson distribution）

设随机变量 $X\in \{0,1,2,\dots \}$。若 $X$ 服从参数为 $\lambda >0$ 的泊松分布，记作 $X\sim \text{Poi}(\lambda )$，则其概率质量函数（pmf）为：

$$\begin{array}{}\text{(2.24)}& \text{Poi}(x\mid \lambda )=\frac{e^{-\lambda }{\lambda }^x}{x!}\end{array}$$

其中，$\lambda$ 是该分布的均值，同时也是方差，即：

$$\mathbb{E}[X]=\text{Var}(X)=\lambda$$

负二项分布（Negative binomial distribution）

假设我们有一个“盒子”（或称“容器”）中有 $N$ 个球，其中：

• $R$ 个是红球

• $B$ 个是蓝球

我们进行有放回抽样，直到抽出 $n\ge 1$ 个球。设 $X$ 表示这 $n$ 个球中蓝球的数量。可以证明：

$$X\sim \text{Bin}(n,p)\text{其中 }p=\frac{B}{N}$$

即：$X$ 服从二项分布。

转换视角：定义失败为红球，成功为蓝球

现在我们重新定义抽红球为“失败”、抽蓝球为“成功”。我们继续抽球，直到观察到 $r$ 次失败（红球）为止。

设 $X$ 表示在这过程中抽到的“成功”次数（即蓝球个数）。可以证明：

$$X\sim \text{NegBinom}(r,p)$$

也就是说，$X$ 服从 负二项分布（Negative binomial distribution），其概率质量函数定义为：

$$\begin{array}{}\text{(2.25)}& \text{NegBinom}(x\mid r,p)\triangleq (\genfrac{}{}{0ex}{}{x+r-1}{x})(1-p{)}^r{p}^x\end{array}$$

其中 $x\in \{0,1,2,\dots \}$，表示成功的次数。

组合数 $(\genfrac{}{}{0ex}{}{x+r-1}{x})$

这表示从 $x+r-1$ 次试验中选出 $x$ 次成功的位置，剩下的是失败。

这里试验顺序重要，且第 $r$ 次失败必须是第 $x+r$ 次试验的结果（最后一次失败）。

• 二项分布关注试验次数固定，成功次数随机。

• 负二项分布关注成功次数固定，试验次数（失败次数）随机。

特殊情况说明

如果 $r$ 是实数，我们将组合数 $(\genfrac{}{}{0ex}{}{x+r-1}{x})$ 替换为伽马函数表达式：

$$(\genfrac{}{}{0ex}{}{x+r-1}{x})=\frac{\mathrm{\Gamma }(x+r)}{x!\cdot \mathrm{\Gamma }(r)}$$

利用了恒等式 $(x-1)!=\mathrm{\Gamma }(x)$。

数学期望与方差

负二项分布的两个矩（均值和方差）为：

$$\begin{array}{}\text{(2.26)}& \mathbb{E}[x]=\frac{pr}{1-p},\text{Var}[x]=\frac{pr}{(1-p{)}^2}\end{array}$$

负二项分布的意义与优势

这种含有两个参数的分布比泊松分布更具有建模灵活性，因为它可以单独控制均值与方差。这在模拟某些“传染性事件”时非常有用，例如某些事件之间是正相关的，它们的出现会导致比独立情形更大的方差。

事实上，泊松分布是负二项分布的一个特例。可以证明：

$$\text{Poi}(\lambda )=\underset{r\to \mathrm{\infty }}{lim}\text{NegBinom}(r,\frac{\lambda }{1+\lambda })$$

另一个特例是当 $r=1$ 时，负二项分布变为几何分布（Geometric distribution）。

定义在实数上的连续分布

在本节中，我们讨论一些定义在实数集合 $\mathbb{R}$ 上的一元连续分布，即 $p(x)$ 且 $x\in \mathbb{R}$。

高斯分布（正态分布）

最广泛使用的一元分布是高斯分布（Gaussian distribution），也叫正态分布（normal distribution）。

高斯分布的概率密度函数（pdf）定义为：

$$\begin{array}{}\text{(2.27)}& \mathcal{N}(x\mid \mu ,{\sigma }^2)\triangleq \frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{1}{2{\sigma }^2}(x-\mu {)}^2)\end{array}$$

其中，$\sqrt{2\pi {\sigma }^2}$ 是归一化常数，用于确保整个密度函数的积分为 1。

• 参数 $\mu$ 表示分布的均值（mean），也是该分布的众数（mode）。

• 参数 ${\sigma }^2$ 表示分布的方差（variance）。

有时我们也会讨论高斯分布的精度（precision），即方差的倒数：$\lambda =1/{\sigma }^2$。

精度越高意味着分布越“窄”（即方差小），集中在 $\mu$ 附近。

高斯分布的累积分布函数（cdf）定义为：

$$\begin{array}{}\text{(2.28)}& \mathrm{\Phi }(x;\mu ,{\sigma }^2)\triangleq {\int }_{-\mathrm{\infty }}^x\mathcal{N}(z\mid \mu ,{\sigma }^2)dz\end{array}$$

如果 $\mu =0$、$\sigma =1$（即所谓的标准正态分布），我们简写为 $\mathrm{\Phi }(x)$。

半正态分布（Half-normal）

在某些问题中，我们希望使用定义在非负实数上的分布。一种构造这类分布的方法是设定：

$$Y=|X|，\text{其中 }X\sim \mathcal{N}(0,{\sigma }^2)$$

由此诱导出的 $Y$ 的分布被称为半正态分布（half-normal distribution），其概率密度函数为：

$$\begin{array}{}\text{(2.29)}& {\mathcal{N}}^{+}(y\mid \sigma )\triangleq 2\mathcal{N}(y\mid 0,{\sigma }^2)=\frac{\sqrt{2}}{\sigma \sqrt{\pi }}\exp (-\frac{y^2}{2{\sigma }^2}),y\ge 0\end{array}$$

这个分布可以被看作是标准正态分布 $\mathcal{N}(0,{\sigma }^2)$ 在 0 处对折（folded over）后的结果。

学生 t 分布（Student t-distribution）

高斯分布的一个问题在于它对离群点非常敏感，因为其概率密度随着与中心的平方距离增大而指数级衰减。一种更具鲁棒性的分布是 学生 t 分布（Student t-distribution），我们简称为Student 分布。它的概率密度函数（pdf）如下：

$$\begin{array}{}\text{(2.30)}& T_{\nu }(x|\mu ,{\sigma }^2)=\frac{1}{Z}{[1+\frac{1}{\nu }{\left(\frac{x-\mu }{\sigma }\right)}^2]}^{-(\nu +1)/2}\end{array}$$

其中：

• $\mu$ 是均值，

• $\sigma >0$ 是尺度参数（注意：不是标准差），

• $\nu >0$ 被称为自由度（不过一个更恰当的术语可能是“正态程度” [Kru13]，因为当 $\nu$ 趋于较大值时，该分布会表现得像高斯分布）。

归一化常数 $Z$ 的表达式为：

$$\begin{array}{}\text{(2.31)}& Z=\sqrt{\nu \pi {\sigma }^2}\cdot \frac{\mathrm{\Gamma }(\nu /2)}{\mathrm{\Gamma }((\nu +1)/2)}=\sqrt{\nu }\cdot \sigma \cdot B(1/2,\nu /2)\end{array}$$

这里：

• $\mathrm{\Gamma }(a)$ 是Gamma 函数，定义为：

$$\begin{array}{}\text{(2.32)}& \mathrm{\Gamma }(a)\triangleq {\int }_0^{\mathrm{\infty }}{x}^{a-1}{e}^{-x}dx\end{array}$$

• $B(a,b)$ 是Beta 函数，定义为：

$$\begin{array}{}\text{(2.33)}& B(a,b)\triangleq \frac{\mathrm{\Gamma }(a)\mathrm{\Gamma }(b)}{\mathrm{\Gamma }(a+b)}\end{array}$$

柯西分布（Cauchy distribution）

当 $\nu =1$ 时，Student 分布被称为 柯西分布（Cauchy distribution） 或 洛伦兹分布（Lorentz distribution）。它的概率密度函数（pdf）定义为：

$$\begin{array}{}\text{(2.34)}& C(x|\mu ,\gamma )=\frac{1}{Z}{[1+{\left(\frac{x-\mu }{\gamma }\right)}^2]}^{-1}\end{array}$$

其中：

• $Z=\gamma \cdot B(1/2,1)=\gamma \pi$，即归一化常数。

这个分布的一个显著特点是：它的尾部非常厚重（heavy tails），以至于定义均值的积分并不收敛（即没有期望值）。

半柯西分布（half Cauchy distribution） 是一种基于均值为 0 的柯西分布进行“折叠”的版本，也就是说，它的概率密度函数全部集中在正实数轴上。

因此，其形式为：

$$\begin{array}{}\text{(2.35)}& C^{+}(x|\gamma )\triangleq \frac{2}{\pi \gamma }{[1+{\left(\frac{x}{\gamma }\right)}^2]}^{-1}\end{array}$$

更多分布使用到的时候再进行补充

高斯联合分布（Gaussian joint distributions）

对于连续型随机变量，使用最广泛的联合概率分布是多元高斯分布（multivariate Gaussian 或 multivariate normal，简称 MVN）。

这种分布之所以受欢迎，一方面是因为其数学处理非常方便，另一方面在许多实际问题中，高斯分布作为近似是相当合理的。事实上，在给定均值和协方差矩的约束下，高斯分布是熵最大的分布。鉴于它的重要性，本节将详细讨论高斯分布。

多元正态分布（The multivariate normal）

在本节中，我们将详细介绍多元高斯分布，又称多元正态分布（MVN）。

定义（Definition）

多元高斯分布的概率密度函数定义如下：

$$\begin{array}{}\text{(2.71)}& \mathcal{N}(\mathbf{x}|\mathit{\mu },\mathbf{\Sigma })\triangleq \frac{1}{(2\pi {)}^{D/2}|\mathbf{\Sigma }{|}^{1/2}}\exp (-\frac{1}{2}(\mathbf{x}-\mathit{\mu }{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathit{\mu }))\end{array}$$

其中：

• $\mathit{\mu }=\mathbb{E}[\mathbf{x}]\in {\mathbb{R}}^D$ 是均值向量，

• $\mathbf{\Sigma }=\text{Cov}[\mathbf{x}]$ 是 $D\times D$ 的协方差矩阵，

• 归一化常数 $Z=(2\pi {)}^{D/2}|\mathbf{\Sigma }{|}^{1/2}$ 保证整个 pdf 的积分为 1。

指数中的表达式（忽略系数 -0.5）是数据向量 $\mathbf{x}$ 相对于均值 $\mathit{\mu }$ 的马氏距离（Mahalanobis distance）平方，定义如下：

$$\begin{array}{}\text{(2.72)}& d_{\mathbf{\Sigma }}^2(\mathbf{x},\mathit{\mu })=(\mathbf{x}-\mathit{\mu }{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathit{\mu })\end{array}$$

在二维空间中，多元高斯分布被称为二维高斯分布（bivariate Gaussian distribution）。其概率密度函数可表示为：

$$\mathbf{x}\sim \mathcal{N}(\mathit{\mu },\mathbf{\Sigma })，\mathrm{其}\mathrm{中}\mathbf{x}\in {\mathbb{R}}^2,\mathit{\mu }\in {\mathbb{R}}^2,$$

协方差矩阵形式为：

$$\begin{array}{}\text{(2.73)}& \mathbf{\Sigma }=\left[\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right]\end{array}$$

其中：

• $\rho$ 是相关系数，定义为：

  $$\rho =\frac{\text{Cov}(x_1,x_2)}{{\sigma }_1{\sigma }_2}$$

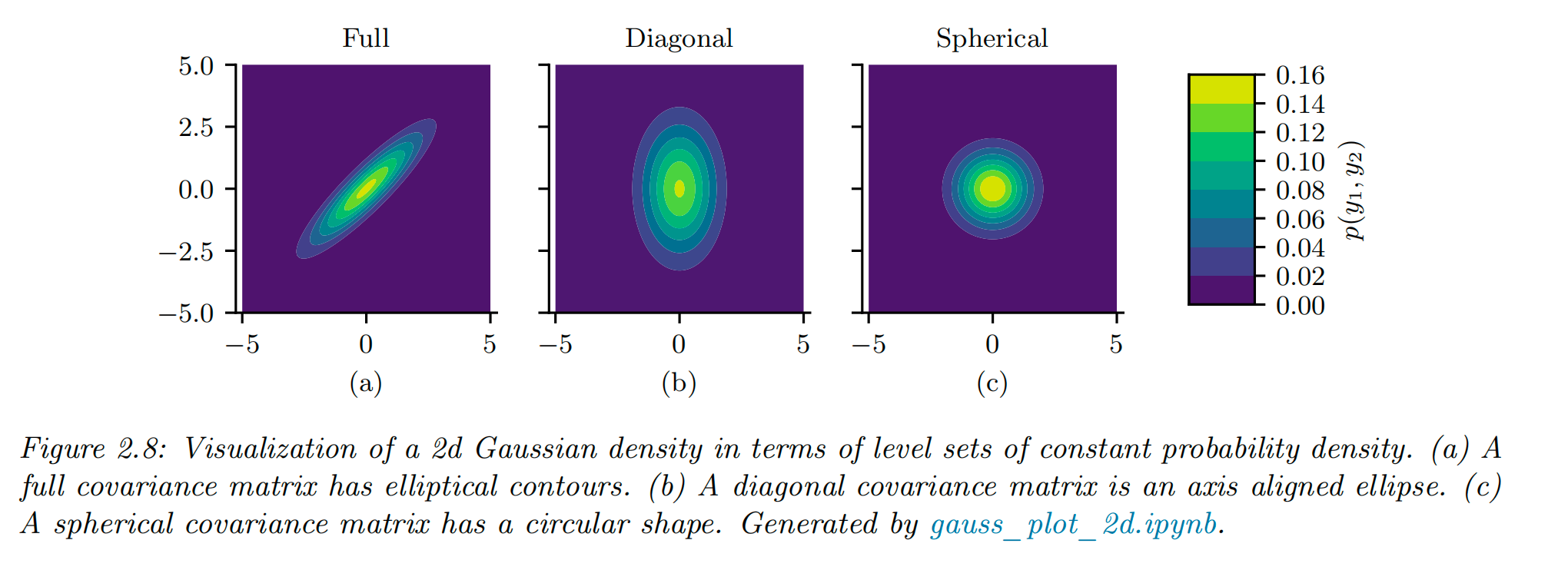
图 2.8 展示了三种不同协方差矩阵下的二维多元高斯密度图：

• 完全协方差矩阵（Full covariance matrix）: 有 $D(D+1)/2$ 个自由参数（由于 $\mathbf{\Sigma }$ 是对称的，所以除以 2）。

• 对角协方差矩阵（Diagonal covariance matrix）: 只有 D 个自由参数，非对角线元素为 0，表示变量之间不相关。

• 球形协方差矩阵（Spherical covariance matrix）: 也称为各向同性协方差矩阵（isotropic covariance matrix），只有一个自由参数 ${\sigma }^2$，表示所有方向的方差相同。

  $$\mathbf{\Sigma }={\sigma }^2{\mathbf{I}}_D$$

  只有一个自由参数 ${\sigma }^2$，表示所有方向的方差相同。

当然可以，以下是你提供内容的逐段翻译与解释，保持原意清晰、结构一致：

---

高斯壳（Gaussian shells）

在高维空间中，多元高斯分布的行为可能会显得非常反直觉。我们可以提出这样一个问题：

如果我们从 $\mathbf{x}\sim \mathcal{N}(0,I_D)$ 中采样，其中 $D$ 是维度数，我们应该预期这些样本大多会落在空间的哪里？

由于概率密度函数的峰值（众数）位于原点 $\mathbf{0}$，我们直觉上会认为：大多数样本应该靠近原点。

然而，在高维空间中，高斯分布的“典型集合（typical set）”实际上是一个很薄的壳层或环带，其：

• 与原点的距离为：

  $$r=\sigma \sqrt{D}$$

• 壳层的厚度为：

  $$O(\sigma D^{1/4})$$

---

直观解释如下：

虽然密度函数以 $e^{-r^2/2}$ 的形式衰减 —— 即离原点越远，密度越小，但与此同时：

• 球体的体积随半径 $r$ 按 $r^D$ 的速率快速增长；

• 因为概率质量 = 密度 × 体积；

• 所以，两者之间会出现一种“相互抵消的平衡点” —— 也就是在某个距离范围内，虽然密度在下降，但体积增加更快；

• 大多数样本会集中在这个区域上 —— 也就是所谓的“高斯肥皂泡现象（Gaussian soap bubble phenomenon）”。

---

数学解释：为什么高斯样本集中在壳层上？

考虑某个点 $\mathbf{x}$ 到原点的平方距离：

$$d(\mathbf{x})=\sqrt{\sum _{i=1}^D{x}_i^2}\text{其中 }{x}_i\sim \mathcal{N}(0,1)$$

1. 期望平方距离为：

   $$\mathbb{E}[d^2]=\sum _{i=1}^D\mathbb{E}[x_i^2]=D$$

2. 方差为：

   $$\mathrm{Var}(d^2)=\sum _{i=1}^D\mathrm{Var}(x_i^2)=D$$

3. 相对标准差（变异系数）为：

   $$\begin{array}{}\text{(2.74)}& \underset{D\to \mathrm{\infty }}{lim}\frac{\mathrm{std}(d^2)}{\mathbb{E}[d^2]}=\underset{D\to \mathrm{\infty }}{lim}\frac{\sqrt{D}}{D}=0\end{array}$$

这意味着：

• 尽管每个样本的距离是随机的；

• 但当维度 $D$ 越大时，它们的平方距离越来越集中在 $D$ 附近；

• 从而，距离本身越来越集中在 $\sqrt{D}$ 附近。

这就是为什么我们说样本会集中在距离原点约为 $\sqrt{D}$ 的薄壳层上。

---

图像空间的含义（例如灰度图像）

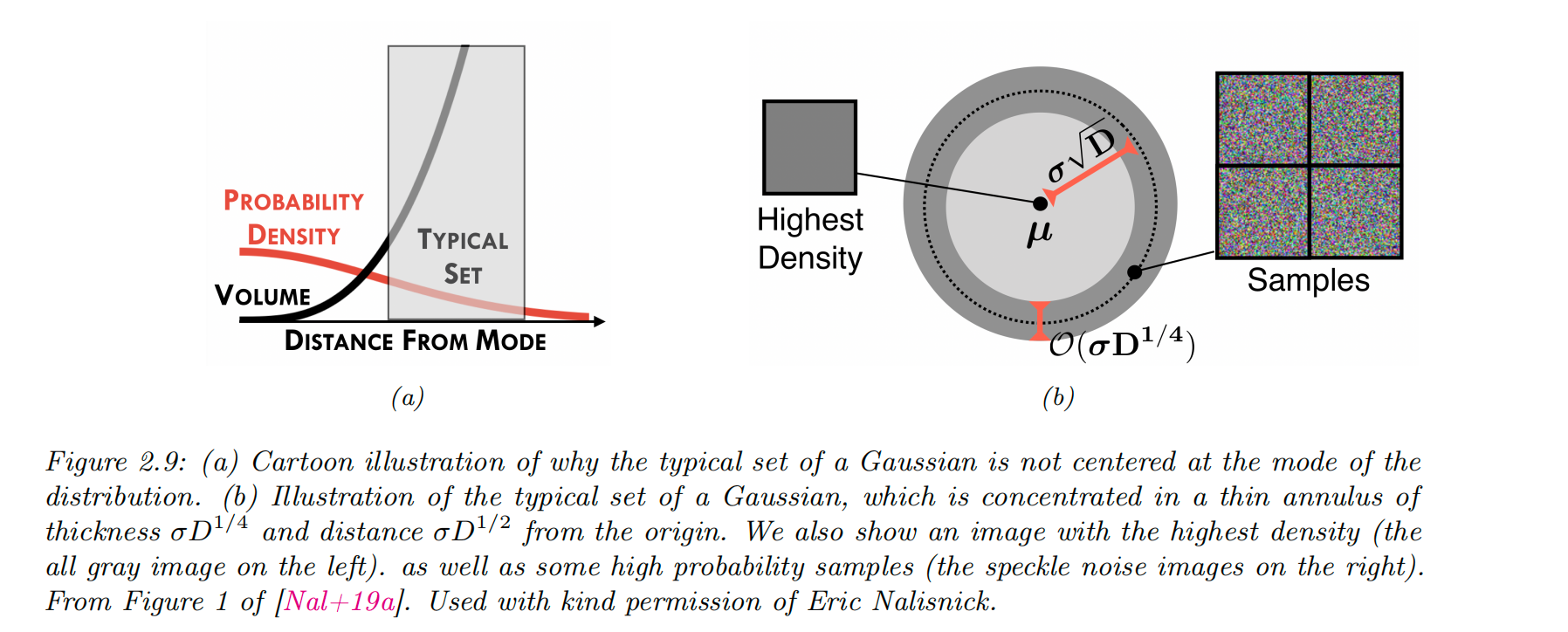
图 2.9b 展示了一些从如下高斯分布中采样的灰度图像：

$$\mathbf{x}\sim \mathcal{N}(\mu ,{\sigma }^{2}I)$$

其中 $\mu$ 是一张“全灰”的图片（每个像素亮度相同）。

你可能以为既然是围绕全灰图采样，那么采样出来的图像应该也接近灰色。但事实恰恰相反：

在高维图像空间中，几乎不可能采样到接近灰色的图像。

这是因为样本几乎全部落在离 $\mu$ 一定距离的“典型壳层”上，而不是密度最大的中心点（即灰色图像）。这非常反直觉，但却是高维高斯的真实现象。