数学知识点

数学知识点

协方差矩阵

协方差是两个变量“是否一起变化”的度量:

• 如果两个变量 一起变大或一起变小，协方差是正的；

• 如果一个变量变大时另一个变小，协方差是负的；

• 如果两个变量 无关，协方差接近 0。

数学定义（以两个变量为例）:

$$\text{cov}(X,Y)=\mathbb{E}[(X-{\mu }_X)(Y-{\mu }_Y)]$$

直观上，它表示：

“X 和 Y 的偏离平均值的乘积”的期望。

扩展到多个变量：协方差矩阵

如果你有 多个变量（如 $x_1,x_2,x_3,...,x_D$），你就可以把它们两两之间的协方差，组成一个 矩阵，这个矩阵就叫：

$$\mathbf{\text{协方差矩阵}}=\mathrm{\Sigma }$$

---

协方差矩阵的结构，以三个变量为例（比如身高、体重、年龄）：

$$\mathrm{\Sigma }=\left[\begin{array}{ccc}\text{cov}(x_1,x_1)& \text{cov}(x_1,x_2)& \text{cov}(x_1,x_3)\\ \text{cov}(x_2,x_1)& \text{cov}(x_2,x_2)& \text{cov}(x_2,x_3)\\ \text{cov}(x_3,x_1)& \text{cov}(x_3,x_2)& \text{cov}(x_3,x_3)\end{array}\right]$$

注意：

• 对角线上的元素：$\text{cov}(x_i,x_i)=\text{var}(x_i)$，也就是每个变量自己的方差。

• 非对角线上的元素：表示变量之间的相关性（协方差）。

• 这个矩阵是 对称的（因为 $\text{cov}(x_i,x_j)=\text{cov}(x_j,x_i)$）。

---

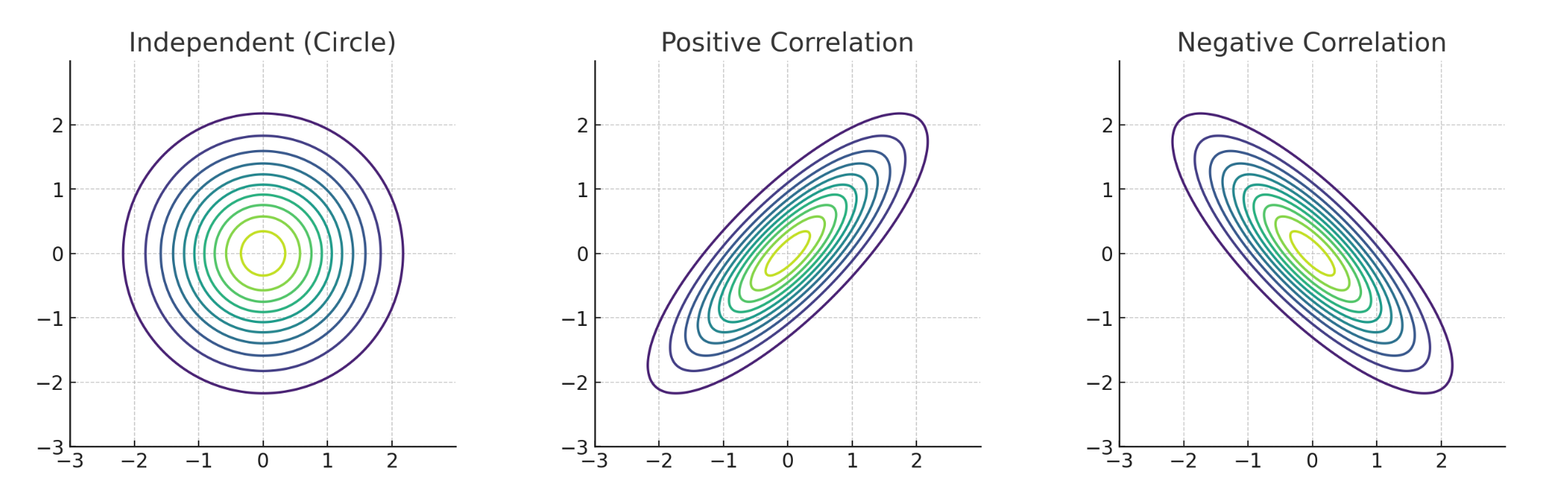
图像直观理解（二维协方差矩阵），如果我们画出一个二维正态分布：

• 当两个变量 不相关，协方差 = 0 → 分布是一个 圆形。

• 当两个变量 正相关，协方差 > 0 → 分布是一个 沿对角线方向拉长的椭圆。

• 当两个变量 负相关，协方差 < 0 → 椭圆朝反对角线方向倾斜。

---

在深度学习与生成模型中，协方差矩阵可以用来：

场景	用法
多元高斯分布	表达不同维度之间的“联合关系”
高斯混合模型（GMM）	不同类别的“形状”和“方向”由协方差控制
马氏距离	衡量点与均值之间的距离，但考虑变量相关性
主成分分析（PCA）	通过协方差矩阵找出“主要变化方向”（特征值分解）
高斯过程（GP）	协方差函数定义样本之间的相似性结构

---

一个例子帮助理解，假设我们有如下样本（身高和体重）：

人	身高（cm）	体重（kg）
A	170	65
B	180	75
C	160	55

先计算每一维的均值，再计算协方差矩阵（不展开计算细节）后，你会得到：

$$\mathrm{\Sigma }=\left[\begin{array}{cc}100& 100\\ 100& 100\end{array}\right]$$

这意味着：

• 身高和体重的方差都为 100；

• 协方差为 100，说明它们强烈正相关。

---

总结:

名词	含义
协方差（cov）	度量两个变量是否同步变化
协方差矩阵（$\mathrm{\Sigma }$）	所有变量两两之间协方差的矩阵表示
对角线	每个变量自己的方差
非对角线	表示不同变量之间的线性相关性
应用	多元高斯、高斯过程、GMM、PCA、马氏距离等

马氏距离

欧几里得距离（Euclidean Distance）

公式是：

$$D_E(x,\mu )=\sqrt{(x-\mu {)}^T(x-\mu )}$$

直观理解：

• 它就是我们平时量两个点之间“直线距离”的方法。

• 它对每个维度的偏差一视同仁，不考虑各维度数据的分布特征。

• 换句话说，哪怕某个维度的数据本来波动很大（方差大），它在这个维度上的偏差也会被直接算入距离，导致整体距离变大。

马氏距离（Mahalanobis Distance）

公式是：

$$D_M(x,\mu )=\sqrt{(x-\mu {)}^T{\mathrm{\Sigma }}^{-1}(x-\mu )}$$

其中 $\mathrm{\Sigma }$ 是数据的协方差矩阵。

直观理解：

• 它不仅考虑两个点之间的差异，还考虑数据在各个维度上的方差大小和维度间的相关性。

• ${\mathrm{\Sigma }}^{-1}$ 是协方差矩阵的逆，起到了“标准化”的作用，把数据的不同尺度和相关性都考虑进来。

尺度差异性

欧几里得距离计算方式：

$$D_E(x,\mu )=\sqrt{(x-\mu {)}^T(x-\mu )}$$

• 它直接对每个维度的偏差做平方加总。

• 如果某个维度的数值范围很大（如年龄：0~100），另一个维度很小（如身高标准化后波动在 $[-1,1]$），那么前者的变化会主导整个距离。

• 这会导致尺度大的特征“支配”了距离判断，从而导致偏差。

---

马氏距离定义如下：

$$D_M(x,\mu )=\sqrt{(x-\mu {)}^T{\mathrm{\Sigma }}^{-1}(x-\mu )}$$

其中 $\mathrm{\Sigma }$ 是样本协方差矩阵，${\mathrm{\Sigma }}^{-1}$ 是它的逆矩阵。

---

假设我们有一个样本点 $x$，均值是 $\mu$，方差是 ${\sigma }^2$，那么协方差矩阵就是：

$$\mathrm{\Sigma }={\sigma }^2,{\mathrm{\Sigma }}^{-1}=\frac{1}{{\sigma }^2}$$

此时马氏距离变为：

$$D_M(x,\mu )=\sqrt{(x-\mu {)}^2\cdot \frac{1}{{\sigma }^2}}=\frac{|x-\mu |}{\sigma }$$

👉 这就是我们熟悉的 标准差单位距离（z-score 距离）。

结论：马氏距离会自动把不同特征的偏差按标准差进行“标准化”。

---

在高维空间中：

• $\mathrm{\Sigma }$ 是一个 $d\times d$ 的协方差矩阵；

• 它包含了每个特征的方差（主对角线），和特征间的协方差（非对角元素）；

• ${\mathrm{\Sigma }}^{-1}$ 相当于一个“加权标准化器”，对不同方向的偏差做缩放和正交旋转。

设两维特征的协方差矩阵是：

$$\mathrm{\Sigma }=\left[\begin{array}{cc}100& 0\\ 0& 1\end{array}\right]\Rightarrow {\mathrm{\Sigma }}^{-1}=\left[\begin{array}{cc}0.01& 0\\ 0& 1\end{array}\right]$$

说明：

• 第一个维度方差是 100，第二个维度方差是 1；

• 马氏距离中对第一个维度的偏差乘上 $0.01$，惩罚少；

• 第二个维度的偏差乘上 1，惩罚多。

这就实现了 对每个维度根据尺度差异进行惩罚调整 —— 偏差大但常见的就不判定为“远”，偏差小但罕见的要严惩。

---

你可以把马氏距离想成是：

“在考虑数据分布形状后，重新拉直空间、拉平数据”的距离度量。

• 原始空间中，数据可能沿某个方向拉长、压扁；

• 马氏距离通过协方差矩阵逆变换，把这些方向“拉回正态”；

• 变换后再用欧几里得距离度量 —— 就能反映“真实统计意义上的远近”。

总结

• 欧几里得距离适合所有维度的尺度和方差差不多时，或者你不在意尺度差异。

• 马氏距离适合不同维度尺度差别大、方差差异大且可能相关的情况，更能反映真实的“统计距离”。