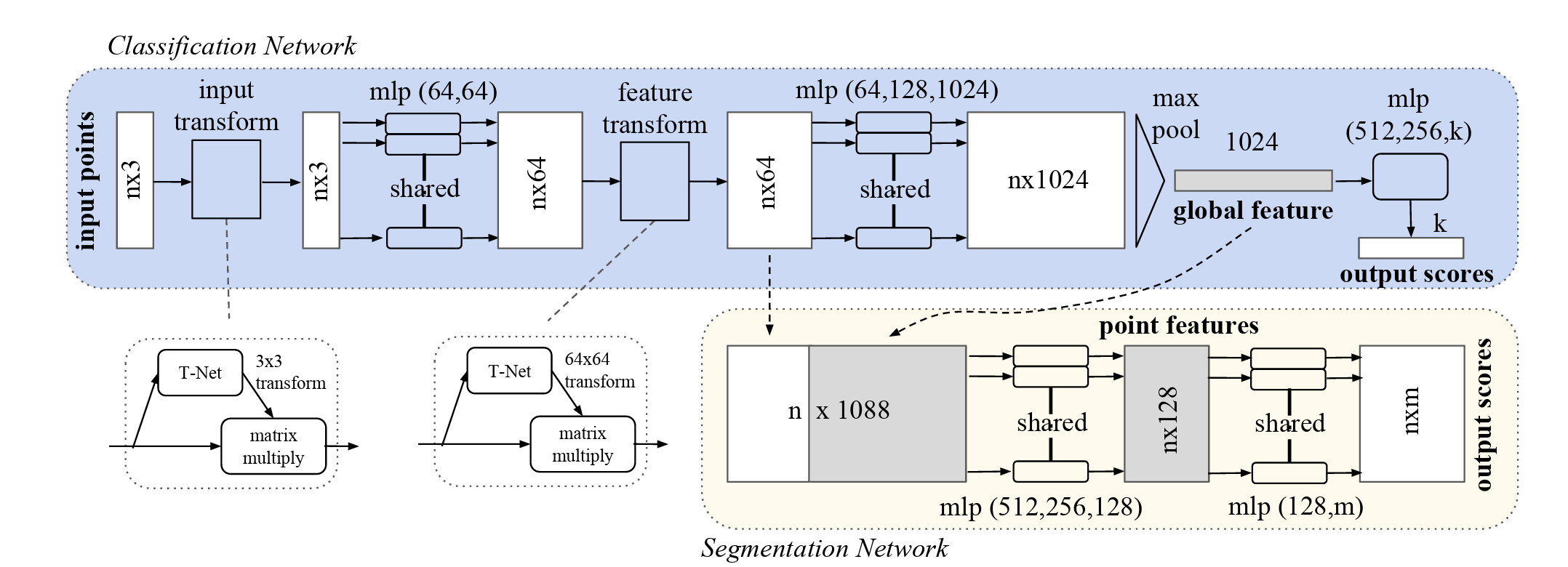
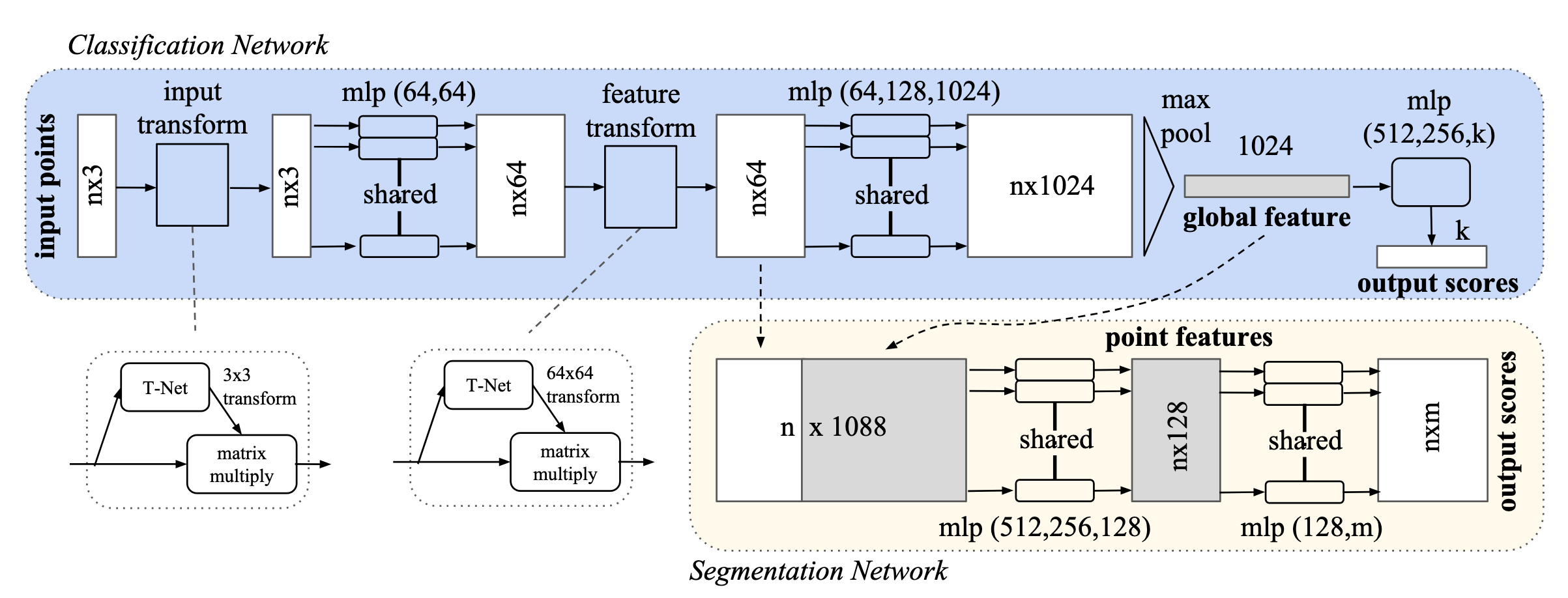
简析PointNet

BinaryOracle2025/5/25大约 20 分钟约 6047 字

简析PointNet网络模型及其背后原理

简析PointNet

论文: https://arxiv.org/abs/1612.00593
TensorFlow 版本代码: https://github.com/charlesq34/pointnet
Pytorch 版本代码: https://github.com/fxia22/pointnet.pytorch

核心

问题背景: 点云是三维几何数据的一种重要表示形式，但由于其无序性和非规则性，传统卷积神经网络难以直接处理。

❌ 传统方法的缺陷：

将点云转换为体素网格（voxel grid）或图像视图（multi-view rendering），这些方法会导致信息损失、计算量大、不灵活等问题。

🌟 PointNet 的创新点：

直接以点集作为输入，避免了复杂的预处理；
设计了一个统一架构，适用于分类、物体分割和场景语义解析；
利用对称函数（如最大池化）实现点集顺序不变性；
引入 T-Net（空间变换网络）标准化输入点云和特征空间。

难点

点云的无序性（Unordered）: 点云是点的集合，没有固定顺序；模型必须对输入点的排列顺序不敏感（permutation invariant）。
点之间存在相互作用（Interaction among points）: 点与点之间有空间关系，需要捕捉局部结构。
对几何变换的不变性（Invariance under transformations）: 模型输出应不受刚性变换影响（如旋转、平移）。
输入点云可能缺失或包含噪声（Missing or noisy points）: 实际采集的点云常有遮挡、稀疏、异常值等问题。

解决方案

✅ 难点 1：点云的无序性 → 使用对称函数（Symmetric Function）

使用 max pooling 作为对称函数，聚合所有点的信息；
所有点经过共享参数的 MLP 提取特征；
最终输出与点的顺序无关；

原理说明：

f({x1, ..., xn}) ≈ g(h(x1), ..., h(xn)) = γ(MAX(h(x1), ..., h(xn)))

其中：

h(xi) 是每个点的高维特征；
MAX 是 max pooling 函数；
γ 是后续的全连接网络；
整个函数 f 是对称的，即对点顺序不敏感。

效果：

实验证明 max pooling 比排序、RNN、average pooling 更有效；s
PointNet 可以处理任意顺序的点集；

✅ 难点 2：点之间的相互作用 → 设计局部 + 全局信息融合机制

在分割任务中，将全局特征与每个点的局部特征拼接起来；
这样每个点在预测标签时都能看到整个物体的上下文；

效果：

显著提升了分割性能；
让模型既关注局部细节，又理解整体结构；

✅ 难点 3：对几何变换的不变性 → 引入 T-Net（空间变换网络）

引入两个空间变换网络：
- STN3d：对输入点云做刚性变换（3×3 矩阵）；
- STNkd：对特征空间做变换（64×64 矩阵）；
加入正则项约束变换矩阵接近正交：

L_reg = ||I - A @ A^T||_F^2

效果：

PointNet 对点云的旋转、平移等变换具有鲁棒性；
提升了模型的泛化能力和稳定性；

✅ 难点 4：输入点云可能缺失或含有异常点 → 理论分析保证模型鲁棒性

理论上证明 PointNet 学到的是一个“关键点集”（critical point set），即只依赖一小部分关键点就能判断整体形状；
即使丢失一些点或加入异常点，只要关键点还在，结果就不会变；

定理表明：

小扰动不会改变函数输出；
网络输出由一个有限子集 CS 决定（大小不超过 bottleneck 维度 K）；
CS 是关键点集合，NS 是最大可容忍的点云范围；

实验验证：

即使 50% 的点缺失，分类准确率仅下降约 3.7%；
对异常点也有一定容忍能力；

✅ 总结: PointNet 通过 max pooling 实现对称性，结合 T-Net 实现变换不变性，并通过局部+全局特征融合机制实现强大的点云建模能力，解决了点云处理中的四大技术难点，为后续三维深度学习奠定了基础。

代码(Pytorch版本)

输入标准化

在 PointNet 架构中，第一层是一个叫做 STN3d（Spatial Transformer Network for 3D points）的模块，它的目标是：

✅ 对输入的点云做刚性变换（如旋转 + 平移），使其姿态统一，提升模型鲁棒性。

这是因为在实际采集过程中，点云的姿态可能各不相同（比如椅子朝向不同、扫描角度不同等），如果不加处理，会影响特征提取的一致性。

STN3d 是一个小型神经网络，专门用于预测一个 3×3 的变换矩阵，这个矩阵表示对点云所做的变换（通常是旋转或反射）。

它具有以下特点：

输入是原始点云（shape: (B, 3, N)）；
输出是一个变换矩阵（shape: (B, 3, 3)）；
这个变换矩阵是近似正交的，保证变换是刚性的；
变换矩阵会通过 torch.bmm() 应用到原始点云上（这一步不在 STN3d 类中）；
目的是让点云“摆正”，便于后续处理。

代码实现:

class STN3d(nn.Module):
    def __init__(self):
        super(STN3d, self).__init__()
        # 使用 1D 卷积 处理点云数据（每个点有 3 个坐标值）
        # kernel_size=1 表示只在通道维度操作，不考虑空间邻域关系
        # 提取每一点的特征向量（从 3 → 64 → 128 → 1024）
        self.conv1 = torch.nn.Conv1d(3, 64, 1)
        self.conv2 = torch.nn.Conv1d(64, 128, 1)
        self.conv3 = torch.nn.Conv1d(128, 1024, 1)

        # 经过全局池化后得到一个全局特征向量（1024维）
        # 用全连接层逐步压缩到 9 个输出 → 对应一个 3x3 的变换矩阵
        self.fc1 = nn.Linear(1024, 512)
        self.fc2 = nn.Linear(512, 256)
        self.fc3 = nn.Linear(256, 9)

        # 所有卷积和 FC 层后面都加了 BN 和 ReLU，帮助训练稳定收敛
        self.relu = nn.ReLU() 
        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(128)
        self.bn3 = nn.BatchNorm1d(1024)
        self.bn4 = nn.BatchNorm1d(512)
        self.bn5 = nn.BatchNorm1d(256)

    # x: (batch,3,point_size)
    def forward(self, x):
        # 获取当前 batch 的大小（有多少组点云）
        batchsize = x.size()[0]
        # CNN 逐点，通道维度特征提取阶段
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = F.relu(self.bn3(self.conv3(x))) # x: (batch,1024,point_size)
        # 全局最大池化（Global Max Pooling）
        # 从所有点中选出每个通道的最大响应值，作为整个点云的“抽象”表示，shape: (B, 1024)
        # 返回：一个元组：(values, indices)，分别是最大值和它们的位置索引。
        x = torch.max(x, 2, keepdim=True)[0] # x: (batch,1024,1)
        x = x.view(-1, 1024) # x: (batch,1024)
        
        # 全连接层预测变换矩阵
        x = F.relu(self.bn4(self.fc1(x)))
        x = F.relu(self.bn5(self.fc2(x)))
        x = self.fc3(x) # x: (batch,9)
         
         # 加上单位矩阵作为初始偏置
         # 初始假设变换为恒等变换（不做任何变化）
        iden = Variable(torch.from_numpy(np.array([1,0,0,0,1,0,0,0,1]).astype(np.float32))).view(1,9).repeat(batchsize,1)
        if x.is_cuda:
            iden = iden.cuda()
        # 让网络从一个小扰动开始学习，更容易训练    
        x = x + iden
        # 最终 reshape 成 3x3 矩阵返回 
        x = x.view(-1, 3, 3)
        return x

标准化的意义:

✅ 1. 解决点云姿态不一致问题

输入点云可能来自不同角度、不同位置；
T-Net 把它们“对齐”到一个标准姿态；
这样 PointNet 后续的特征提取更稳定。

✅ 2. 提升模型鲁棒性

如果没有 T-Net，PointNet 必须自己学会对各种姿态都识别准确；
加入 T-Net 后，相当于加了一个“预处理层”，让模型更容易训练和泛化。

神经网络的输出在训练初期往往接近于零，如果直接作为变换矩阵，会导致非正交、不稳定。PointNet 通过“加单位矩阵”的方式，让变换矩阵从一个恒等变换开始学习，并结合正则化损失，逐步向正交矩阵靠拢，从而保证变换是刚性的、稳定的。

正则化损失

feature_transform_regularizer 是 PointNet 中用于约束变换矩阵接近正交性的正则化损失函数。

🧠 为什么需要这个正则化项？

在 PointNet 中，为了提升模型对点云姿态变化的鲁棒性，引入了两个变换网络：

STN3d: 对原始点云做刚性变换（如旋转、反射），使其标准化。
STNkd: 对特征空间做变换，使特征分布更稳定。

这两个网络输出的是变换矩阵（分别是 3×3 和 k×k 的矩阵）。但由于它们是神经网络直接预测出来的，并不能保证这些矩阵是正交矩阵（orthogonal matrix）。

❗而只有正交矩阵才能表示刚性变换（rigid transformation），即只改变物体的方向而不改变形状和大小。

所以我们需要加一个正则化项来鼓励变换矩阵接近正交矩阵 , 这就是 feature_transform_regularizer 的作用！

def feature_transform_regularizer(trans):
    d = trans.size()[1]
    batchsize = trans.size()[0]
    # 构造一个单位矩阵 I，用于后续比较；
    # 添加 None 是为了扩展成 (1, d, d)，便于广播到整个 batch；
    I = torch.eye(d)[None, :, :]
    if trans.is_cuda:
        I = I.cuda()
    # 计算变换矩阵与其转置相乘后与单位矩阵之间的距离（Frobenius 范数），然后取 batch 平均值作为损失项，鼓励变换矩阵接近正交矩阵。 
    # Frobenius 范数（矩阵所有元素平方和开方）   
    loss = torch.mean(torch.norm(torch.bmm(trans, trans.transpose(2,1)) - I, dim=(1,2)))
    return loss

特征提取

PointNet 的核心特征提取模块 PointNetfeat ，它负责从输入点云中提取出可用于分类或分割的特征。

class PointNetfeat(nn.Module):
    def __init__(self, global_feat = True, feature_transform = False):
        super(PointNetfeat, self).__init__()
        # 输入点云变换网络（3D）
        self.stn = STN3d()

        # 使用 Conv1D 对每个点进行特征提取；
        # 每个卷积层后跟一个 BatchNorm 层；
        # 最终输出高维特征（1024维）；
        self.conv1 = torch.nn.Conv1d(3, 64, 1)
        self.conv2 = torch.nn.Conv1d(64, 128, 1)
        self.conv3 = torch.nn.Conv1d(128, 1024, 1)
        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(128)
        self.bn3 = nn.BatchNorm1d(1024)

        # 全局特征开关：控制是否输出全局特征
        self.global_feat = global_feat
        # 特征变换开关：控制是否使用 STN 对特征空间进行变换
        self.feature_transform = feature_transform
        if self.feature_transform:
            self.fstn = STNkd(k=64)

    def forward(self, x):
        n_pts = x.size()[2]
        # 使用 STN3d 预测出一个变换矩阵；
        trans = self.stn(x)
        x = x.transpose(2, 1)
        # 将原始点云“摆正”；
        x = torch.bmm(x, trans)
        x = x.transpose(2, 1)
        # 再通过第一个卷积层提取初始特征；
        x = F.relu(self.bn1(self.conv1(x)))
        
        if self.feature_transform:
            trans_feat = self.fstn(x)
            x = x.transpose(2,1)
            x = torch.bmm(x, trans_feat)
            x = x.transpose(2,1)
        else:
            trans_feat = None

        # 提取更高维的特征；
        # 最后一层输出 shape: (B, 1024, N) 
        pointfeat = x
        x = F.relu(self.bn2(self.conv2(x)))
        x = self.bn3(self.conv3(x))
        # 从所有点中选出每个通道的最大响应值，作为整个点云的“抽象”表示，shape: (B, 1024)
        # 返回：一个元组：(values, indices)，分别是最大值和它们的位置索引。        
        x = torch.max(x, 2, keepdim=True)[0]
        x = x.view(-1, 1024)
        # 如果是分类任务 (global_feat=True)：
        if self.global_feat:
            return x, trans, trans_feat
        else:
        # 如果是分割任务 (global_feat=False)：  
            x = x.view(-1, 1024, 1).repeat(1, 1, n_pts)
            return torch.cat([x, pointfeat], 1), trans, trans_feat

✅ 如果是分类任务 (global_feat=True)，则返回：

x: 全局特征 (B, 1024)
trans: 输入点云变换矩阵
trans_feat: 特征空间变换矩阵（可选）

✅ 如果是分割任务 (global_feat=False)，则返回：

把全局特征复制 N 次并与每个点的局部特征，在通道维度进行拼接
将每个点的局部特征与整个点云的全局特征拼接起来，让每个点都能看到上下文信息
输出 shape: (B, 1088, N) ，即 1088 = 1024+64

分类任务

PointNet 的分类模块 PointNetCls ，它基于前面的特征提取模块 PointNetfeat 来完成点云分类任务。

class PointNetCls(nn.Module):
    def __init__(self, k=2, feature_transform=False):
        super(PointNetCls, self).__init__()
        self.feature_transform = feature_transform
        # 它使用 PointNetfeat 提取全局特征（1024维）；
        self.feat = PointNetfeat(global_feat=True, feature_transform=feature_transform)
        # 然后通过全连接层（MLP）将这些特征映射到类别空间；
        self.fc1 = nn.Linear(1024, 512)
        self.fc2 = nn.Linear(512, 256)
        self.fc3 = nn.Linear(256, k)
        self.dropout = nn.Dropout(p=0.3)
        self.bn1 = nn.BatchNorm1d(512)
        self.bn2 = nn.BatchNorm1d(256)
        self.relu = nn.ReLU()

    def forward(self, x):
        # 它使用 PointNetfeat 提取全局特征（1024维）；
        x, trans, trans_feat = self.feat(x)
        # 然后通过全连接层（MLP）将这些特征映射到类别空间；
        x = F.relu(self.bn1(self.fc1(x)))
        x = F.relu(self.bn2(self.dropout(self.fc2(x))))
        x = self.fc3(x)
        # 最终输出每个类别的概率分布（log_softmax）；
        return F.log_softmax(x, dim=1), trans, trans_feat

分割任务

PointNet 的分割模块 PointNetDenseCls ，它基于前面的特征提取模块 PointNetfeat 来完成点云物体分割任务。

class PointNetDenseCls(nn.Module):
    def __init__(self, k = 2, feature_transform=False):
        super(PointNetDenseCls, self).__init__()
        self.k = k
        self.feature_transform=feature_transform
        self.feat = PointNetfeat(global_feat=False, feature_transform=feature_transform)
        self.conv1 = torch.nn.Conv1d(1088, 512, 1)
        self.conv2 = torch.nn.Conv1d(512, 256, 1)
        self.conv3 = torch.nn.Conv1d(256, 128, 1)
        self.conv4 = torch.nn.Conv1d(128, self.k, 1)
        self.bn1 = nn.BatchNorm1d(512)
        self.bn2 = nn.BatchNorm1d(256)
        self.bn3 = nn.BatchNorm1d(128)

    def forward(self, x):
        batchsize = x.size()[0]
        n_pts = x.size()[2] # 点的数量
        # 调用 PointNetfeat 提取特征
        # 最后将每个点的局部特征与整个点云的全局特征拼接起来，让每个点都能看到上下文信息 
        x, trans, trans_feat = self.feat(x)
        # 使用多层 Conv1D 层进一步融合局部 + 全局信息
        # 最终输出 shape: (B, k, N)
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = F.relu(self.bn3(self.conv3(x)))
        x = self.conv4(x)
        # shape: (B, k, N) -> (B, N, k) , 即每个点的各个类别得分
        x = x.transpose(2,1).contiguous()
        # 使用 log_softmax 得到 log 概率分布；
        x = F.log_softmax(x.view(-1,self.k), dim=-1) # shape: (B*N, k)
        x = x.view(batchsize, n_pts, self.k) # shape: (B, N, k)
        return x, trans, trans_feat

✅ 1. 每个点都需要全局上下文

仅靠局部特征很难判断某个点属于哪个部件（比如椅子的腿 vs 座位）；
加上全局特征后，相当于告诉模型：“你知道吗，这是一个椅子”；
这样模型就能根据上下文更准确地做出判断；

✅ 2. 全局特征不能直接用于分割

全局特征只有一份（(B, 1024)），无法直接用于每个点；
所以要把它复制 N 次，变成 (B, 1024, N)；
再与每个点的局部特征拼接；

缺陷

🧠 一、核心问题：忽略局部结构信息

PointNet 只通过 max pooling 聚合所有点的信息，忽略了局部邻域之间的结构关系。

🔍 原因分析：

PointNet 对每个点独立处理（参数共享），然后使用全局最大池化（Global Max Pooling）提取特征；
这种设计使得网络只关注“最显著的点”，而没有建模点与点之间的局部几何关系；
导致模型无法捕捉到更细粒度的几何细节，比如边缘、曲率、表面纹理等；

💡 论文中的验证：

在部件分割任务中，虽然 PointNet 表现不错，但在一些复杂区域（如椅子腿和桌面连接处）容易出错；
分类任务中对缺失点具有一定鲁棒性，但遇到遮挡严重或点分布不均匀时性能下降明显；

📉 二、分割任务依赖拼接机制，不够精细

PointNet 的分割模块通过拼接全局特征 + 局部特征实现上下文感知，但这种方式表达能力有限。

🔍 原理回顾：

PointNet 的分割网络将全局特征复制 N 次并与每个点的局部特征拼接；
然后使用 Conv1D 进行分类；
实际上是用一个固定大小的全局特征去“广播”给每个点；

⚠️ 问题所在：

全局特征不能很好地反映每个点的上下文；
拼接方式缺乏动态调整机制；
难以区分语义相近但位置不同的区域（如桌子边缘 vs 中心）；

🧱 三、对局部形状变化敏感

PointNet 提取的关键点集合（critical point set）可能不足以代表复杂的局部结构。

🔍 实验观察：

在论文中提到，PointNet 学到的是一个关键点集合，这些点大致构成物体的骨架；
如果这些关键点缺失或被遮挡，即使其他点都在，也可能导致错误分类；
对于非刚性变形（如人体姿态变化），PointNet 的表现不如基于图结构的模型；

📈 四、分类性能略逊于多视角方法

在某些标准数据集（如 ModelNet40）上，PointNet 的分类准确率略低于 MVCNN 等基于图像的方法。

方法	分类准确率
MVCNN（多视角 CNN）	90.1%
VoxNet（体素 CNN）	85.9%
PointNet	89.2%

虽然 PointNet 在速度和效率上占优，但在精度上仍略逊一筹。

🧩 五、难以捕捉非刚性变换下的不变性

PointNet 使用 T-Net 强制学习正交变换矩阵，只能处理刚性变换（旋转、反射），无法处理非刚性形变（如弯曲、拉伸）。

🔍 举例说明：

如果你有一张人脸的点云，由于表情不同，面部发生形变；
PointNet 很难在这种情况下保持分类的一致性；
相比之下，基于图卷积或注意力机制的模型更能捕捉这种非刚性变化；

🧱 六、缺乏层次化特征提取机制

PointNet 是一种单尺度网络，无法像 CNN 那样逐层提取多层次的抽象特征。

✅ 后续改进：

PointNet++ 正是对这一缺陷的改进；
它引入了局部区域搜索 + 多尺度聚合机制；
从而能够更好地捕捉点云的局部结构和层次信息；

📊 七、对稀疏点云敏感

当输入点云非常稀疏时（如只有几十个点），PointNet 的性能会显著下降。

🔍 原因分析：

PointNet 的全局特征来自于 max pooling；
如果点太少，max pooling 得到的特征可能无法覆盖整个物体；
特别是在遮挡严重的情况下，关键点可能丢失；

📐 八、结构简单，不利于高维空间建模

PointNet 的结构过于简单，难以建模更高维度的空间关系。

✅ 后续发展：

后续的 3D 深度学习模型（如 DGCNN、SpiderCNN、PointCNN、Transformer-based 点云模型）都尝试引入更复杂的结构来提升建模能力；
如：构建点之间的邻接图、使用 attention、引入多尺度采样等；

🧪 九、理论上的限制：受限于瓶颈维度 K

PointNet 的表达能力受 max pooling 层维度 K 的限制，即 bottleneck dimension。

📌 来自论文的理论分析：

Theorem 2 表明，PointNet 的输出仅由一个不超过 K 个点的子集决定（critical point set），这意味着：
如果 K 不够大，PointNet 可能遗漏重要细节；
如果 K 太大，又会导致计算资源浪费；

🧱 十、对噪声点敏感（尤其未训练时）

虽然 PointNet 对少量异常点有一定鲁棒性，但如果训练时没有加入扰动，面对大量噪声点时效果较差。

🔍 实验验证：

论文中做了“插入异常点”的实验；
结果显示，如果训练过程中加入了噪声，模型表现良好；
否则，异常点会影响分类和分割性能；

📉 十一、在大规模场景理解任务中表现一般

PointNet 的时间复杂度虽然是 O(N)，但在处理超大规模点云时，仍然不如分块处理或多层级聚合模型高效。

✅ 后续改进方向：

使用分块策略（chunking）
构建点云的层次化表示
引入 attention 或图结构增强局部建模能力

🧩 总结表格：PointNet 的主要缺陷

缺陷类型	描述	是否被后续模型改进
忽略局部结构	仅靠 max pooling 提取特征，无局部聚合机制	✅ PointNet++ 改进
分割精度不高	拼接机制不够精细，缺乏动态上下文感知	✅ Transformer-based 改进
无法处理非刚性变形	T-Net 只学正交变换，无法应对弯曲、拉伸等形变	✅ 图卷积、attention 改进
分类精度略低	在 ModelNet40 上略低于 MVCNN	✅ 多视角 + PointNet 混合模型改进
稀疏点云下性能差	少量点无法覆盖关键结构	✅ PointNet++ 改进
局部建模能力弱	无法捕捉边缘、曲率等细节	✅ DGCNN、SpiderCNN 改进
对噪声点敏感	未经扰动训练时，对异常点鲁棒性差	✅ 加入数据增强后缓解
结构单一	缺乏层次化、多尺度建模能力	✅ PointNet++ / Transformer 改进

📈 PointNet 的优势 vs 缺陷对比

维度	优势	缺陷
输入形式	支持原始点云，无需预处理	无法有效利用局部结构
排列不变性	完全支持	无法区分顺序信息（如时间序列点云）
变换不变性	支持刚性变换标准化	无法处理非刚性形变
分类性能	接近 SOTA	略逊于多视角 CNN
分割性能	表现良好	缺乏精细建模
效率	极其高效（O(N)）	无法充分利用 GPU 并行优化
扩展性	易于扩展为检测、检索等任务	表达能力受限于 max pooling 维度

✅ 一句话总结：

PointNet 的最大缺陷在于它“看不清细节”，只关注全局结构，忽视局部邻域关系，这使得它在细粒度识别、非刚性变形、稀疏点云等任务中表现受限，但它也为后续模型奠定了基础。

背景知识扫盲(可选)

点云

点云: 是一种表示三维空间中物体或场景的方式，它由大量带有位置信息的点组成。

每个点通常包含：

坐标信息：x, y, z（3D 空间中的位置）。
可选属性：颜色（RGB）、法向量（Normal）、强度（Intensity）、时间戳等。

表示形式:

点云（Point Cloud）: 原始点集合：每个点有(x, y, z)坐标; 可选颜色、法向量等属性, 简洁、轻便; 保留原始几何信息,无序性、非结构化、难以用 CNN 处理。
体素网格 (voxel grids) : 将空间划分成立方体格子，每个格子表示是否有物体; 结构规整，适合 3D CNN; 计算复杂度高、稀疏性强、精度受限。
多视角图像（Multi-View Images）: 从多个角度渲染点云或 3D 模型为 2D 图像; 可使用成熟的 2D CNN 方法; 丢失部分几何信息，依赖视角选择。
网格（Mesh）：由三角形面片组成的 3D 模型；包含表面细节，适合渲染；难以自动构建，拓扑复杂。

对称函数

对称函数（Symmetric Function）是一种对输入顺序不敏感的函数；换句话说，无论你如何打乱输入元素的顺序，输出结果都保持不变。

🧠 数学定义:

设 $f (x_{1}, x_{2}, . . ., x_{n})$ 是一个函数，如果对于任意排列 $σ$ （permutation），都有：

f (x_{1}, x_{2}, . . ., x_{n}) = f (x_{σ (1)}, x_{σ (2)}, . . ., x_{σ (n)})

那么 $f$ 就是一个 对称函数。

PointNet 处理的是点云数据，而点云是无序集合（unordered set），即：

点云中点的顺序不影响整体形状。
所以模型必须具有对点顺序的不变性（permutation invariance）。
这就要求网络中的某些关键操作必须是对称函数，才能保证整个网络输出与输入点的顺序无关。

📦 常见的对称函数:

函数	描述	是否可微	应用场景
最大池化（Max Pooling）	取所有点的最大值： $max (x_{1}, x_{2}, . . ., x_{n})$	✅ 是	PointNet 中的核心操作
平均池化（Average Pooling）	取所有点的平均值： $\frac{1}{n} \sum_{i = 1}^{n} x_{i}$	✅ 是	特征融合、平滑处理
求和（Summation）	所有点相加： $\sum x_{i}$	✅ 是	构建全局特征向量
乘积（Product）	所有点相乘： $\prod x_{i}$	⚠️ 对数值变化敏感	不常用，但可用于特定任务
最小池化（Min Pooling）	取最小值： $min (x_{1}, x_{2}, . . ., x_{n})$	✅ 是	异常检测等特殊场景
Softmax + 加权和（Attention-based Sum）	根据注意力机制加权求和，权重由 softmax 得出	✅ 是	DGCNN、Transformer 中使用
统计量（如方差、标准差）	计算点集的分布特性	✅ 是	特征增强、异常检测
集合函数近似器（如 Deep Sets）	使用神经网络直接学习对称函数	✅ 是	更复杂的对称函数建模

刚性运动

刚性运动(rigid motions) 是指：物体在空间中移动时，其形状和大小保持不变的运动方式 。

刚性运动	❌ 不改变	移动、旋转
非刚性运动	✅ 改变	弯曲、拉伸、缩放（非均匀）、变形

刚性运动 = 平移 + 旋转，不改变物体形状和内部结构，只改变位置和朝向。

正交变换

正交变换的本质是：只改变物体的方向（旋转），不改变形状和大小

所以：

正交变换包括：旋转 + 反射。
不包括：缩放、剪切、拉伸等会导致形变的操作。