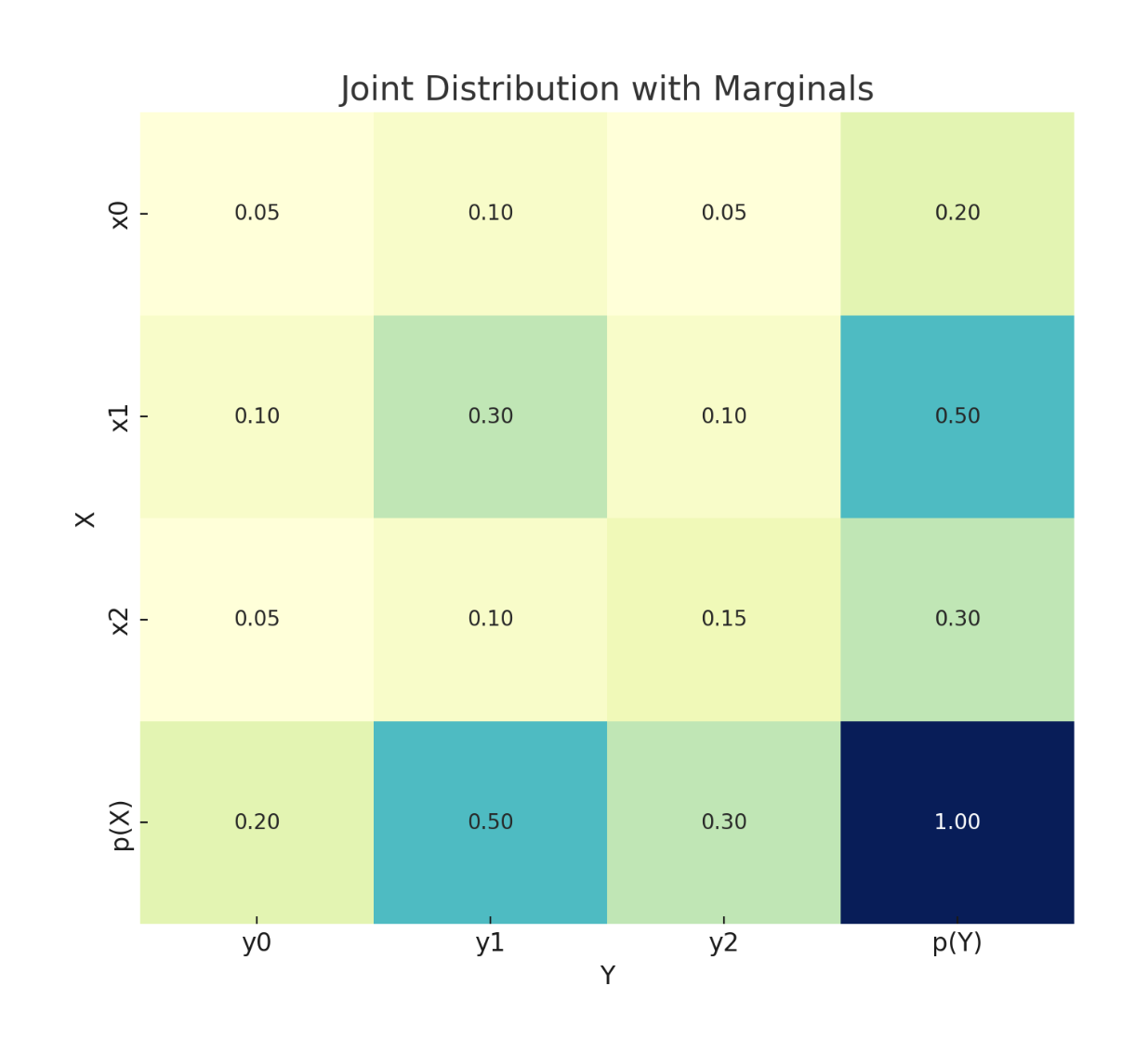
概率论基础模型(用到多少,学多少 =_=)
Bayes' rule
Question One: What's the mean of Bayesian inference ?
“推理”(inference)是指“从样本数据出发,得出带有一定置信度的一般性结论的行为”。术语“贝叶斯”(Bayesian)则用来指代那些使用概率理论来表示“置信度”(即确定程度)并利用 贝叶斯公式(Bayes’ rule) 根据观察数据更新置信度的方法。
贝叶斯公式本身非常简单:它是一个用于计算在给定观测数据
这个公式可以由以下恒等式直接推出:
而这个恒等式又来自于概率的乘法法则(product rule)。
在公式 (2.51) 中,术语
术语
将先验概率
通过对每个
我们可以用一句话来总结贝叶斯公式:
这里使用符号
使用贝叶斯公式,根据观测数据对某一感兴趣的未知量的分布进行更新的过程,被称为贝叶斯推理(Bayesian inference)或后验推理(posterior inference),也可以简称为概率推理(probabilistic inference)。
Bayes 公式人话版本: “先有预期 + 接收信息 → 更新判断”
Inverse problems
概率论的核心是:在已知世界状态
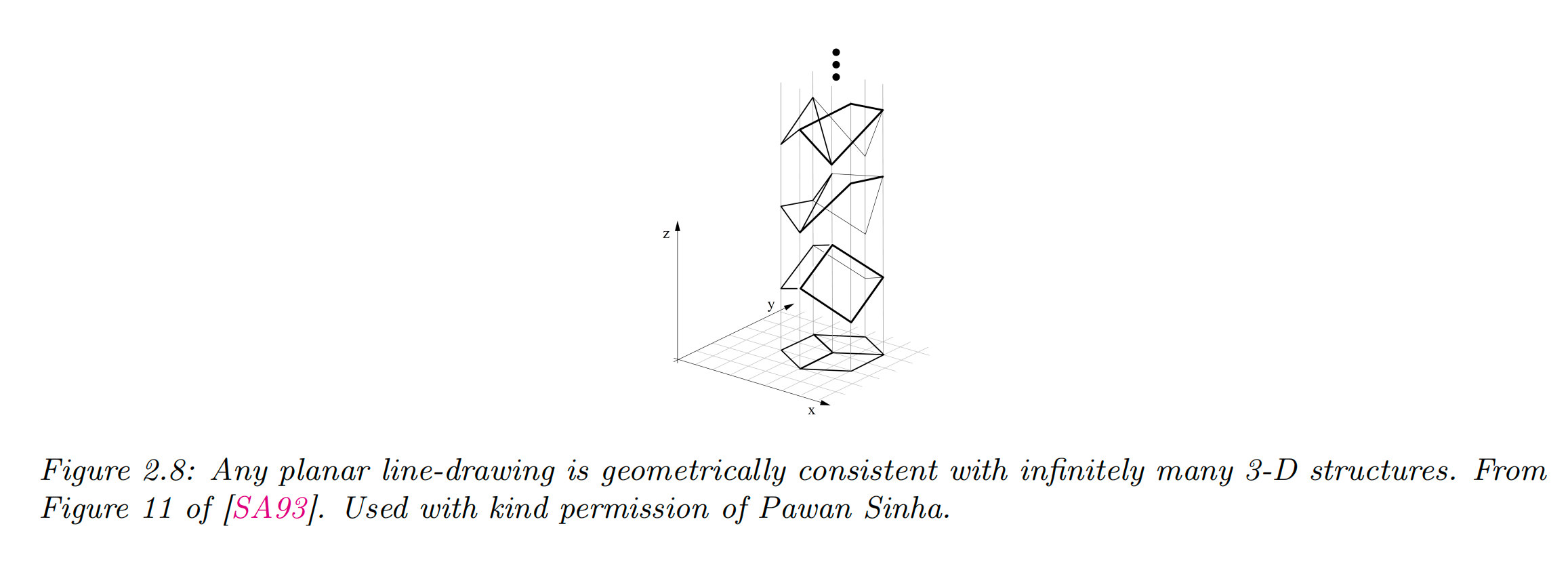
举个例子,设想我们要从一张二维图像
为了解决这类反向问题,我们可以使用贝叶斯公式来计算后验概率
要实现这一点,需要给出:
前向模型
先验分布
混合分布概率模型
混合模型的假设是:观测数据
公式:
其中:
整体
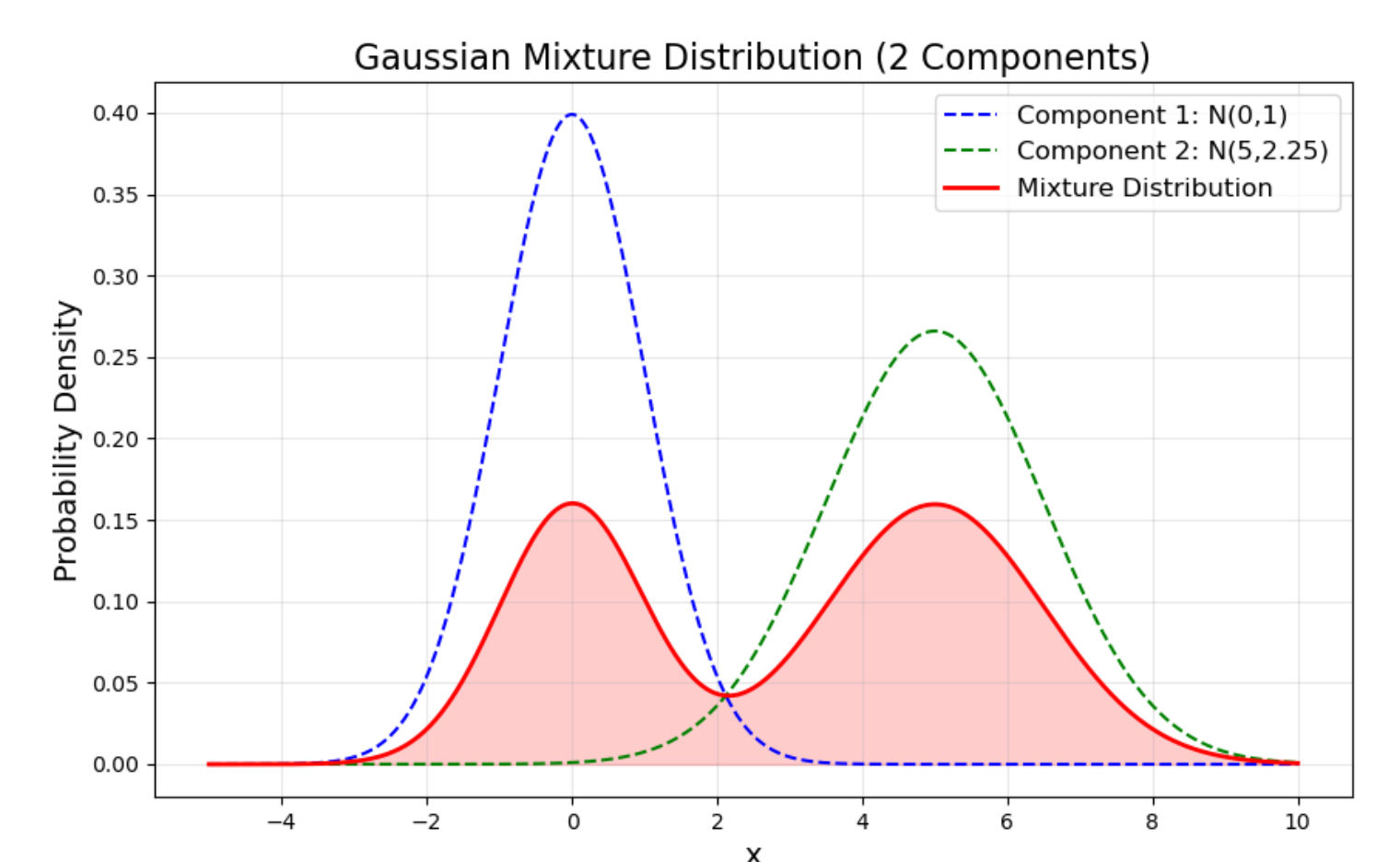
这里列举一个混合高斯分布的例子,我们设定了两个高斯分布:
成分1:均值
成分2:均值
最终的混合分布由这两个分布加权得到:
图中蓝色虚线是第一个高斯,绿色虚线是第二个高斯,红色实线就是它们的混合分布。
这相当于我们有两种“人群”——比如说一部分人身高在 170cm 左右(成分1),另一部分人身高在 180cm 左右(成分2),总人口分布就是这两类人混在一起的结果。这就是混合分布的意义。
在混合分布(Mixture Distribution)里,权重
比如在我举的例子里:
权重必须满足:
权重不是随便定的,它们一般通过 模型假设 + 数据估计 得到:
先验假设:有时我们事先知道(比如男女比例是 50/50),就可以直接设定。
参数学习:如果我们不知道比例,就用算法(通常是 EM算法)在数据上估计。
在 E 步:计算每个样本属于各个分布的“责任值”
在 M 步:根据这些责任值重新估计权重
一旦有了权重
这就是一个新的合法概率分布,可以直接用来:
绘图(像我画的红色曲线)
采样(先按权重选一个分布,再从那个分布里抽样)
计算概率(比如某个损失值出现的概率是多少)
为了更清晰地建模,通常引入一个 隐变量
条件分布
于是:
这就是混合分布的“生成过程”描述。
给定观测
这就是 贝叶斯公式。在标签噪声建模里,这个概率就对应 “一个样本是干净/噪声的可能性”。
期望最大化(Expectation-Maximization, EM)算法
在统计建模里,我们有一组观测数据
这就是 极大似然估计:
通常我们假设数据是 独立同分布(i.i.d.) 的,也就是说:
于是得到:
在混合分布模型中,单个样本的边缘概率是
所以完整似然就是:
混合模型的训练目标是 最大化似然:
直接优化很难,因为里面有求和。常见方法是 期望最大化(Expectation-Maximization, EM)算法:
E步(Expectation):计算后验概率
M步(Maximization):更新参数
更新混合系数:
更新成分参数
不断迭代 E-M,直到收敛。
高斯混合分布模型
高斯混合模型是一种 概率模型,用于对数据进行建模和聚类。它假设数据由 多个高斯分布(正态分布)混合而成,每个高斯分布代表一个潜在的子群体(cluster)。
数学上,GMM 可以写作:
其中:
核心思想:每个样本点
都有一定概率属于每个高斯分布(软聚类),而不是像 K-Means 那样直接划入某个簇(硬聚类)。
Beta 分布
Beta 分布是一类定义在 区间
其概率密度函数(PDF)为:
其中
参数含义
均值和方差为
特殊情况
- 当
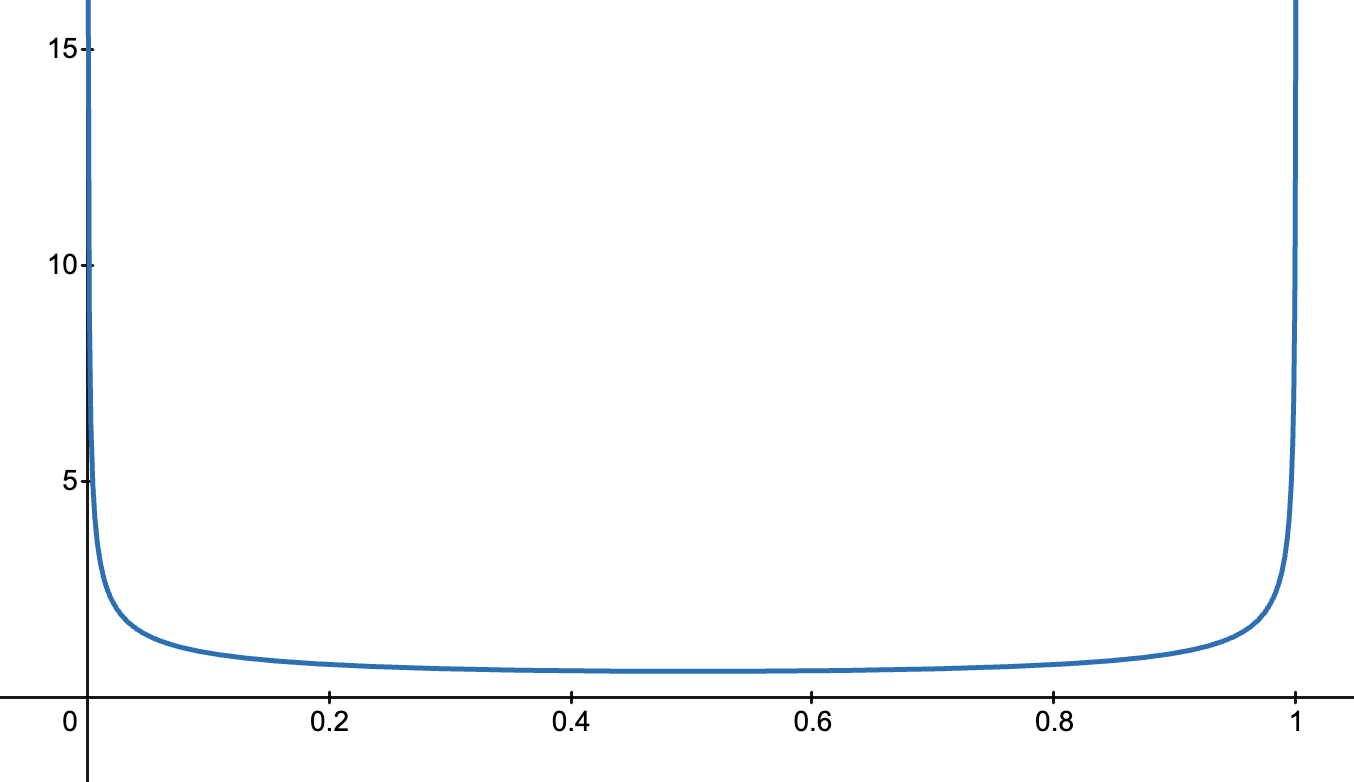
- 当
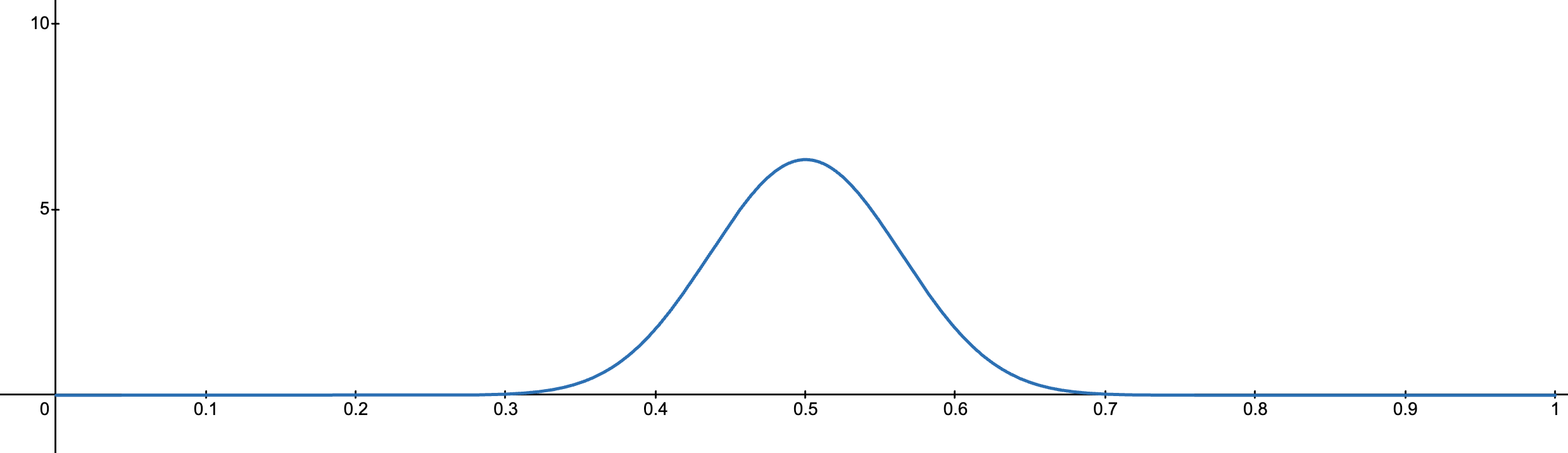
- 当
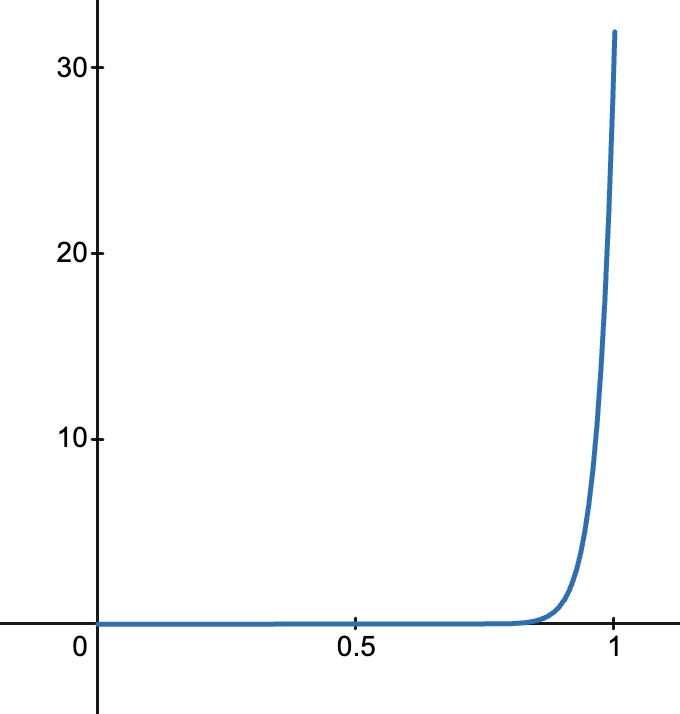
- 当
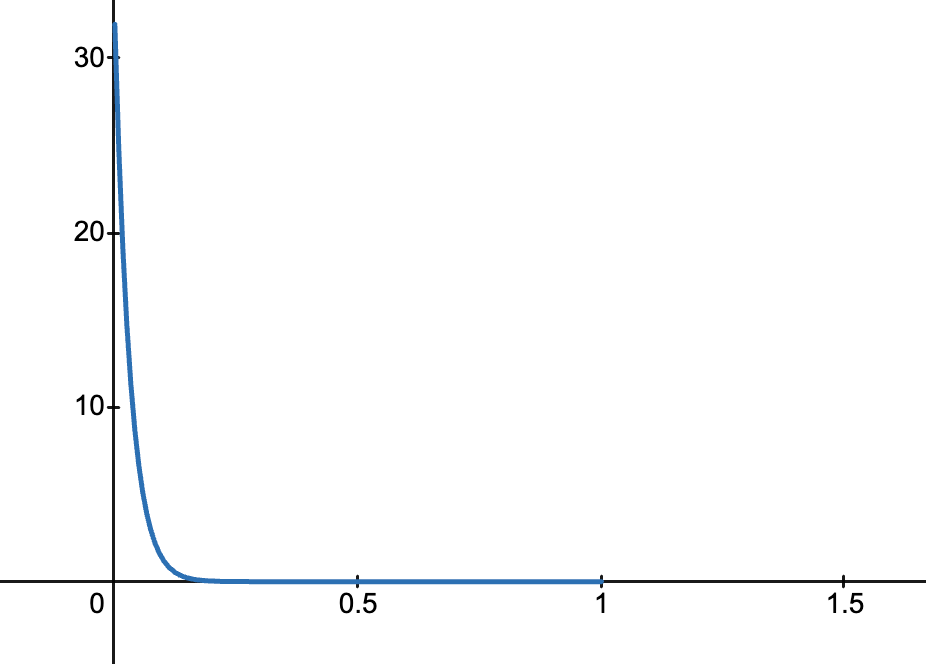
- 当
与二项分布/贝叶斯的关系
Beta 分布常被称为 二项分布的共轭先验。
如果我们有
假设成功概率
那么后验分布也是一个 Beta 分布:
这就是 Beta 分布在贝叶斯学习中的重要性。
Beta 分布的一个超能力是:用它作为二项分布的先验,看到数据之后,它的形式不变(还是 Beta 分布),只需要把参数加上观测次数就行,非常方便。
在机器学习中的应用
(1) 标签噪声建模
- 用 Beta 分布拟合样本损失的分布,可以区分「干净样本」和「噪声样本」。
(2) Mixup 数据增强
- 从
(3) 探索-利用问题(Bandit 问题)
- 在强化学习/多臂老虎机问题中,Beta 分布经常作为成功率的后验。
(4) 概率建模
- 因为 Beta 分布限制在
直观理解
可以把 Beta 分布看作是 “在 0 到 1 之间对概率值的信心”:
例如:
Beta 分布是定义在
互信息
互信息衡量 两个随机变量之间共享的信息量,也就是知道一个变量的信息后,能减少对另一个变量的不确定性多少。
直观理解:
如果两个变量完全独立,互信息为 0。
如果两个变量完全相关(知道一个就能确定另一个),互信息最大。
数学定义
设随机变量 (X) 和 (Y):
离散型:
连续型:
其中:
与熵的关系
互信息也可以表示为熵的形式:
其中:
互信息本质上是“减掉条件不确定性”的熵差。
特性
非负性:
对称性:
独立性:若
共轭先验
在贝叶斯统计中:
先验分布(Prior):表示在观察数据之前,对参数的信念。
似然函数(Likelihood):观测数据给定参数的概率。
后验分布(Posterior):观测数据后,参数的更新分布,根据贝叶斯公式:
共轭先验指的是:
如果选择某个先验分布,使得后验分布和先验分布属于同一分布家族,这个先验就叫共轭先验。
换句话说,共轭先验让 先验 + 数据 → 后验 的形式保持简单、同类。
直观理解
简单例子:投硬币
设投硬币概率 (p) 未知。
观测 (n) 次,得到 (k) 次正面:
如果选择 Beta 分布作为 (p) 的先验:
后验依然是 Beta 分布:
直觉:
Beta 分布“方便匹配”二项分布的形式,让更新后依然是 Beta。
这样计算后验和预测就非常简单,不需要复杂积分。
为什么重要
简化贝叶斯计算:后验易求解析解。
保持分布形式一致:便于连续更新数据。
在机器学习和统计建模中广泛应用,例如:
Dirichlet 是 Multinomial 的共轭先验(LDA 中常用)
Gamma 是 Poisson 的共轭先验
Normal 是 Normal(均值已知方差) 的共轭先验
共轭先验 = 选择一种先验,使得更新后(观测数据后)的后验分布依然属于同一个分布家族。
分布
多项分布(Categorical 分布)
定义:单次试验,选择
记法:
特点:
单次实验
输出是一个类别
特殊情况:当
多项式分布(Multinomial 分布)
定义:多次独立的 Categorical 试验的结果计数。
记法:
特点:
输出是一个计数向量 (
Categorical 是 Multinomial 的单次特例 (
公式:
特点:
输出是一个计数向量 (
Categorical 是 Multinomial 的单次特例 (
Beta 分布
定义:连续分布,用于建模 概率
记法:
特点:
支持单个概率参数的先验
是 Bernoulli/Binomial 分布的 共轭先验
公式:
Dirichlet 分布
定义:多维概率向量的分布,是 Beta 分布的多维推广。
记法:
特点:
支持概率向量 (
是 Multinomial 分布的 共轭先验
公式:
直觉:
Beta 分布对应 (K=2) 的 Dirichlet
Dirichlet 可以看作 Beta 分布在多类别上的推广
关系总结
| 分布类型 | 变量类型 | 实验次数 | 共轭先验 / 后验 |
|---|---|---|---|
| Categorical | 离散类别 ( | 1 | Dirichlet(K≥2) |
| Multinomial | 类别计数向量 ( | N | Dirichlet(K≥2) |
| Bernoulli | 二分类(0/1) | 1 | Beta |
| Binomial | 0/1 次数 | N | Beta |
| Beta | 概率 | — | — |
| Dirichlet | 概率向量 ( | — | — |
关键理解:
单次 vs 多次:
Categorical → 单次多项选择
Multinomial → 多次多项选择
一维 vs 多维:
Beta → 二分类概率的一维先验
Dirichlet → 多分类概率的多维先验
贝叶斯联系:
Beta 是 Bernoulli/ Binomial 的共轭先验
Dirichlet 是 Multinomial/ Categorical 的共轭先验
