VQ-VAE 论文解读与代码实现

BinaryOracle2025/8/1大约 22 分钟约 6493 字

VQ-VAE 论文解读与代码实现

引言

近两年，有许多图像生成类任务的前沿工作都使用了一种叫做"codebook"的机制。追溯起来，codebook机制最早是在VQ-VAE论文中提出的。相比于普通的VAE，VQ-VAE能利用codebook机制把图像编码成离散向量，为图像生成类任务提供了一种新的思路。VQ-VAE的这种建模方法启发了无数的后续工作，包括声名远扬的Stable Diffusion。

在这篇文章中，我将先以易懂的逻辑带领大家一步一步领悟VQ-VAE的核心思想，再介绍VQ-VAE中关键算法的具体形式，最后把VQ-VAE的贡献及其对其他工作的影响做一个总结。通过阅读这篇文章，你不仅能理解VQ-VAE本身的原理，更能知道如何将VQ-VAE中的核心机制活学活用。

从 AE 到 VQ-VAE

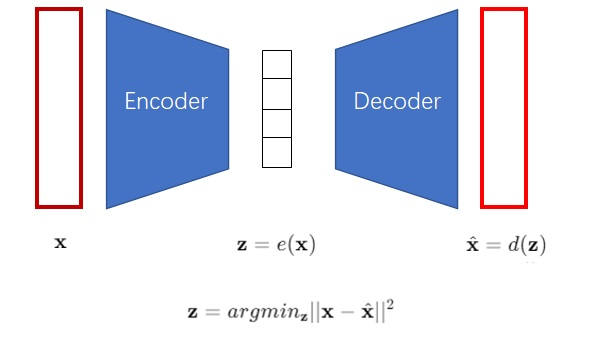
为什么VQ-VAE想要把图像编码成离散向量？让我们从最早的自编码器（Autoencoder, AE）开始一步一步谈起。AE是一类能够把图片压缩成较短的向量的神经网络模型，其结构如下图所示。AE包含一个编码器 $e ()$ 和一个解码器 $d ()$ 。在训练时，输入图像 $x$ 会被编码成一个较短的向量 $z$ ，再被解码回另一幅长得差不多的图像 $\hat{x}$ 。网络的学习目标是让重建出来的图像 $\hat{x}$ 和原图像 $x$ 尽可能相似。

解码器可以把一个向量解码成图片。换一个角度看，解码器就是一个图像生成模型，因为它可以根据向量来生成图片。那么，AE可不可以用来做图像生成呢？很可惜，AE的编码器编码出来的向量空间是不规整的。也就是说，解码器只认识经编码器编出来的向量，而不认识其他的向量。如果你把自己随机生成出来的向量输入给解码器，解码器是生成不出有意义的图片的。AE不能够随机生成图片，所以它不能很好地完成图像生成任务，只能起到把图像压缩的作用。

AE离图像生成只差一步了。只要AE的编码空间比较规整，符合某个简单的数学分布（比如最常见的标准正态分布），那我们就可以从这个分布里随机采样向量，再让解码器根据这个向量来完成随机图片生成了。VAE就是这样一种改进版的AE。它用一些巧妙的方法约束了编码向量，使得满足标准正态分布。这样，解码器不仅认识编码器编出的向量，还认识其他来自标准正态分布的向量。训练完成后，我们就可以扔掉编码器，用来自标准正态分布的随机向量和解码器来实现随机图像生成了。

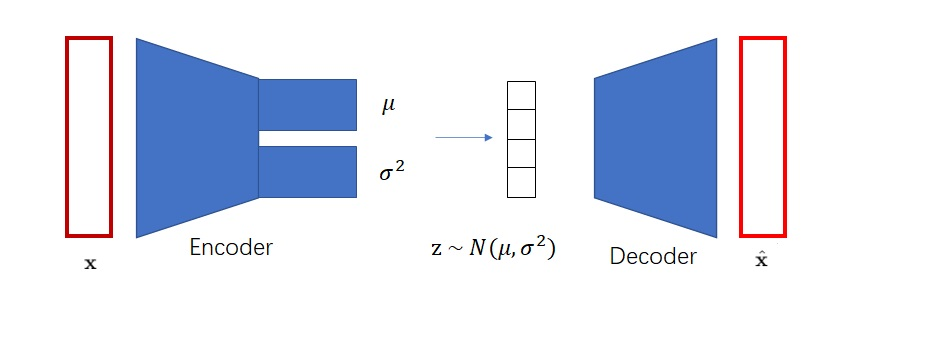
VAE的实现细节就不在这里赘述了，是否理解它对理解VQ-VAE没有影响。我们只需知道VAE可以把图片编码成符合标准正态分布的向量即可。让向量符合标准正态分布的原因是方便随机采样。同时，需要强调的是，VAE编码出来的向量是连续向量，也就是向量的每一维都是浮点数。如果把向量的某一维稍微改动0.0001，解码器还是认得这个向量，并且会生成一张和原向量对应图片差不多的图片。

但是，VAE生成出来的图片都不是很好看。VQ-VAE的作者认为，VAE的生成图片之所以质量不高，是因为图片被编码成了连续向量。而实际上，把图片编码成离散向量会更加自然。比如我们想让画家画一个人，我们会说这个是男是女，年龄是偏老还是偏年轻，体型是胖还是壮，而不会说这个人性别是0.5，年龄是0.6，体型是0.7。因此，VQ-VAE会把图片编码成离散向量，如下图所示。

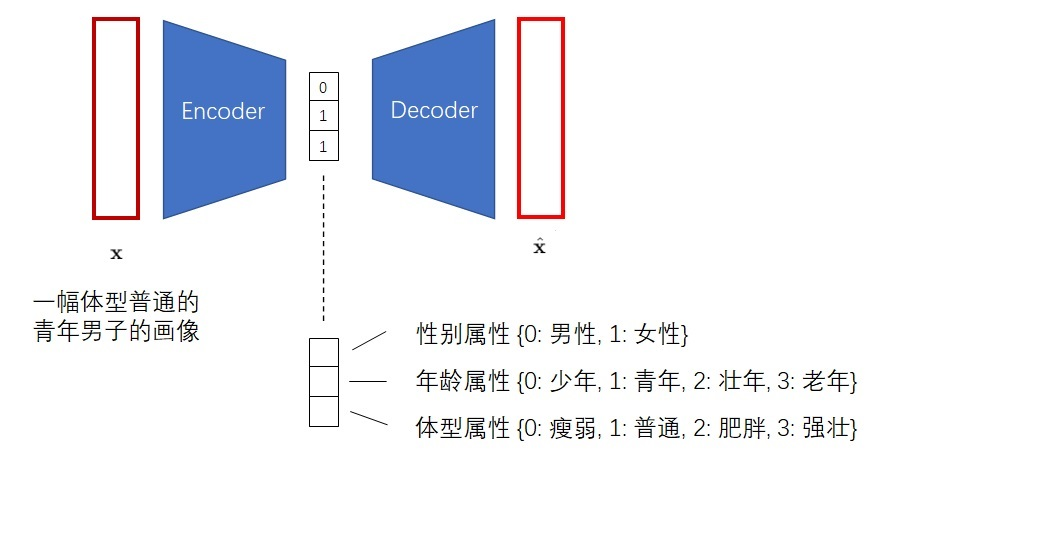
把图像编码成离散向量后，又会带来两个新的问题。第一个问题是，神经网络会默认输入满足一个连续的分布，而不善于处理离散的输入。如果你直接输入0, 1, 2这些数字，神经网络会默认1是一个处于0, 2中间的一种状态。为了解决这一问题，我们可以借鉴NLP中对于离散单词的处理方法。为了处理离散的输入单词，NLP模型的第一层一般都是词嵌入层，它可以把每个输入单词都映射到一个独一无二的连续向量上。这样，每个离散的数字都变成了一个特别的连续向量了。

我们可以把类似的嵌入层加到VQ-VAE的解码器前。这个嵌入层在VQ-VAE里叫做"embedding space（嵌入空间）"，在后续文章中则被称作"codebook"。

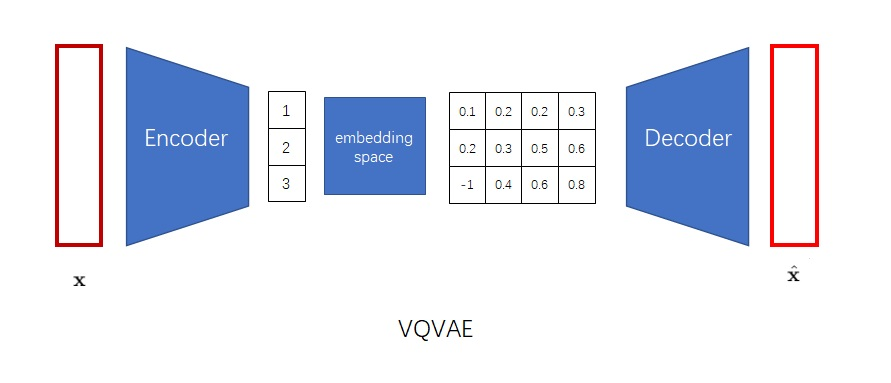
离散向量的另一个问题是它不好采样。回忆一下，VAE之所以把图片编码成符合正态分布的连续向量，就是为了能在图像生成时把编码器扔掉，让随机采样出的向量也能通过解码器变成图片。现在倒好，VQ-VAE把图片编码了一个离散向量，这个离散向量构成的空间是不好采样的。VQ-VAE不是面临着和AE一样的问题嘛。

这个问题是无解的。没错！VQ-VAE根本不是一个图像生成模型。它和AE一样，只能很好地完成图像压缩，把图像变成一个短得多的向量，而不支持随机图像生成。VQ-VAE和AE的唯一区别，就是VQ-VAE会编码出离散向量，而AE会编码出连续向量。

可为什么VQ-VAE会被归类到图像生成模型中呢？这是因为VQ-VAE的作者利用VQ-VAE能编码离散向量的特性，使用了一种特别的方法对VQ-VAE的离散编码空间采样。VQ-VAE的作者之前设计了一种图像生成网络，叫做PixelCNN。PixelCNN能拟合一个离散的分布。比如对于图像，PixelCNN能输出某个像素的某个颜色通道取0~255中某个值的概率分布。这不刚好嘛，VQ-VAE也是把图像编码成离散向量。换个更好理解的说法，VQ-VAE能把图像映射成一个「小图像」。我们可以把PixelCNN生成图像的方法搬过来，让PixelCNN学习生成「小图像」。这样，我们就可以用PixelCNN生成离散编码，再利用VQ-VAE的解码器把离散编码变成图像。

让我们来整理一下VQ-VAE的工作过程。

训练VQ-VAE的编码器和解码器，使得VQ-VAE能把图像变成「小图像」，也能把「小图像」变回图像。
训练PixelCNN，让它学习怎么生成「小图像」。
随机采样时，先用PixelCNN采样出「小图像」，再用VQ-VAE把「小图像」翻译成最终的生成图像。

到这里，我们已经学完了VQ-VAE的核心思想。让我们来总结一下。VQ-VAE不是一个VAE，而是一个AE。它的目的是把图像压缩成离散向量。或者换个角度说，它提供了把大图像翻译成「小图像」的方法，也提供了把「小图像」翻译成大图像的方法。这样，一个随机生成大图像的问题，就被转换成了一个等价的随机生成一个较小的「图像」的问题。有一些图像生成模型，比如PixelCNN，更适合拟合离散分布。可以用它们来完成生成「小图像」的问题，填补上VQ-VAE生成图片的最后一片空缺。

VQ-VAE 实现细节

在上一节中，我们虽然认识了VQ-VAE的核心思想，但略过了不少实现细节，比如：

VQ-VAE的编码器怎么输出离散向量。
VQ-VAE怎么优化编码器和解码器。
VQ-VAE怎么优化嵌入空间。

在这一节里，我们来详细探究这些细节。

输出离散编码

想让神经网络输出一个整数，最简单的方法是和多分类模型一样，输出一个Softmax过的概率分布。之后，从概率分布里随机采样一个类别，这个类别的序号就是我们想要的整数。比如在下图中，我们想得到一个由3个整数构成的离散编码，就应该让编码器输出3组logit，再经过Softmax与采样，得到3个整数。

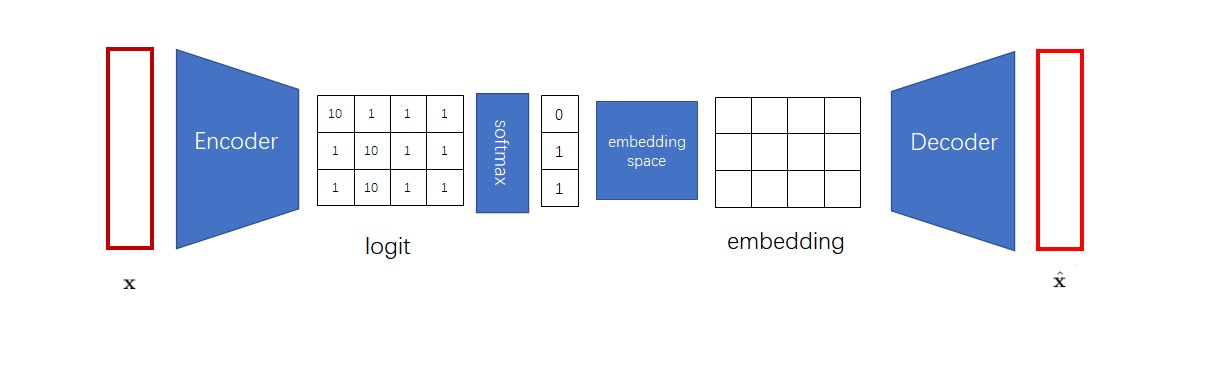
但是，这么做不是最高效的。得到离散编码后，下一步我们又要根据嵌入空间把离散编码转回一个向量。可见，获取离散编码这一步有一点多余。能不能把编码器的输出张量（它之前的名字叫logit）、解码器的输入张量embedding、嵌入空间直接关联起来呢？

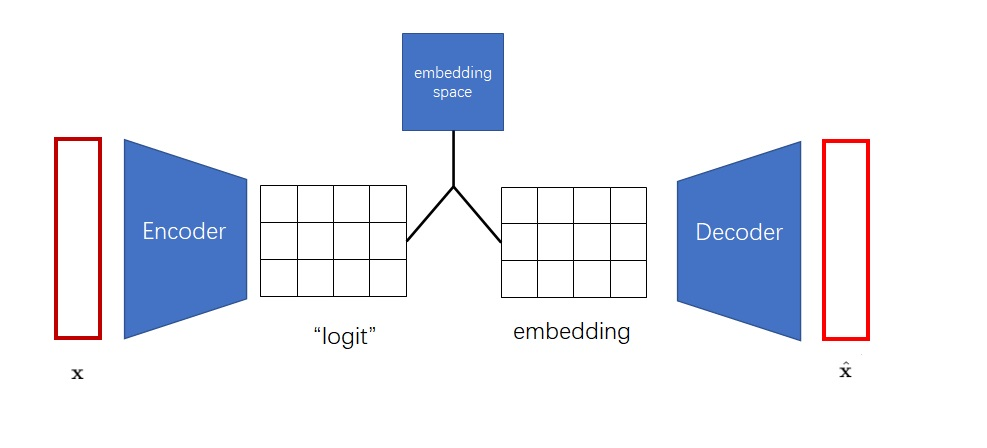
VQ-VAE 使用了如下方式关联编码器的输出与解码器的输入：假设嵌入空间已经训练完毕，对于编码器的每个输出向量 $z_{e} (x)$ ，找出它在嵌入空间里的最近邻 $z_{q} (x)$ ，把 $z_{e} (x)$ 替换成 $z_{q} (x)$ 作为解码器的输入。

求最近邻，即先计算向量与嵌入空间 $K$ 个向量每个向量的距离，再对距离数组取一个 argmin，求出最近的下标（比如图中的 $0, 1, 1$ ），最后用下标去嵌入空间里取向量。下标构成的数组（比如图中的 $[0, 1, 1]$ ）也正是 VQ-VAE 的离散编码。

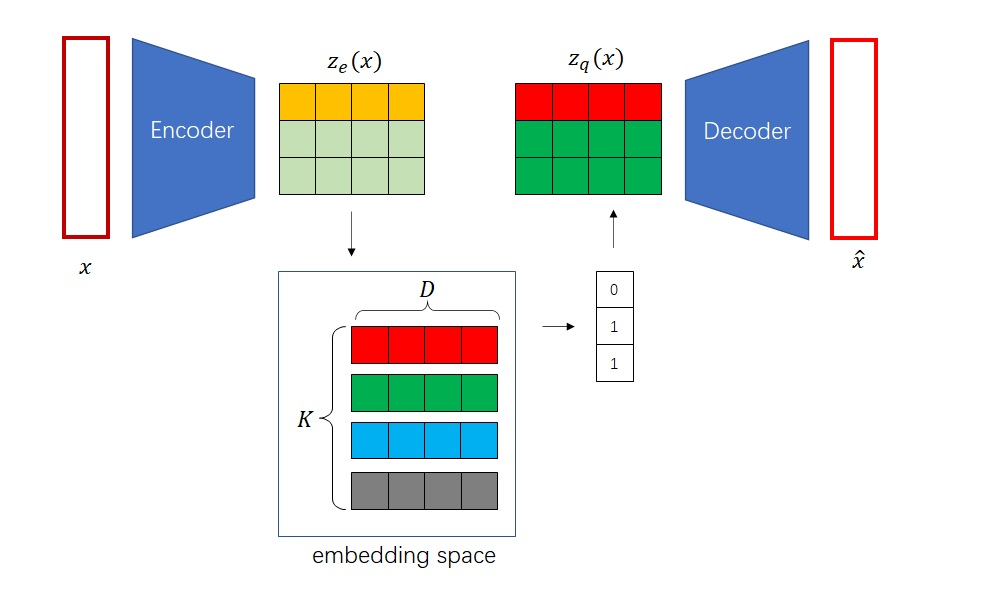
就这样，我们知道了 VQ-VAE 是怎么生成离散编码的。VQ-VAE 的编码器其实不会显式地输出离散编码，而是输出了多个「假嵌入」 $z_{e} (x)$ 。之后，VQ-VAE 对每个 $z_{e} (x)$ 在嵌入空间里找最近邻，得到真正的嵌入 $z_{q} (x)$ ，把 $z_{q} (x)$ 作为解码器的输入。

虽然我们现在能把编码器和解码器拼接到一起，但现在又多出了一个问题：怎么让梯度从解码器的输入 $z_{q} (x)$ 传到 $z_{e} (x)$ ? 从 $z_{e} (x)$ 到 $z_{q} (x)$ 的变换是一个从数组里取值的操作，这个操作是求不了导的。我们在下一小节里来详细探究一下怎么优化 VQ-VAE 的编码器和解码器。

优化编码器和解码器

为了优化编码器和解码器，我们先来制订一下 VQ-VAE 的整体优化目标。由于 VQ-VAE 其实是一个 AE，误差函数里应该只有原图像和目标图像的重建误差。

或者非要从 VAE 的角度说也行。VQ-VAE 相当于输出了一个 one-hot 离散分布。假设输入图像 $x$ 的离散编码 $z$ 是 $k$ ，则分布中仅有 $q (z = k | x) = 1$ ， $q (z = o t h e r s | x) = 0$ 。令离散编码 $z$ 的先验分布是均匀分布（假设不知道输入图像 $x$ ，每个离散编码取到的概率是等同的），则先验分布 $q (z)$ 和后验分布 $q (z | x)$ 的 KL 散度是常量。因此，KL 散度项不用算入损失函数里。理解此处的数学推导意义不大，还不如直接理解成 VQ-VAE 其实是一个 AE。

L_{reconstruct} = ∥ x - decoder (z_{q} (x)) ∥^{2}

但直接拿这个误差来训练是不行的。误差中， $z_{q} (x)$ 是解码器的输入。从编码器输出 $z_{e} (x)$ 到 $z_{q} (x)$ 这一步是不可导的，误差无法从解码器传递到编码器上。要是可以把 $z_{q} (x)$ 的梯度直接原封不动地复制到 $z_{e} (x)$ 上就好了。

VQ-VAE 使用了一种叫做"straight-through estimator"的技术来完成梯度复制。这种技术是说，前向传播和反向传播的计算可以不对应。你可以为一个运算随意设计求梯度的方法。基于这一技术，VQ-VAE 使用了一种叫做 $s g$ （stop gradient，停止梯度）的运算：

s g (x) = {\begin{cases} x & (in forward propagation) \\ 0 & (in backward propagation) \end{cases}

也就是说，前向传播时，sg 里的值不变；反向传播时，sg 按值为 0 求导，即此次计算无梯度。（反向传播其实不会用到式子的值，只会用到式子的梯度。反向传播用到的 loss 值是在前向传播中算的）。

基于这种运算，我们可以设计一个把梯度从 $z_{e} (x)$ 复制到 $z_{q} (x)$ 的误差：

L_{reconstruct} = ∥ x - decoder (z_{e} (x) + s g (z_{q} (x) - z_{e} (x))) ∥_{2}^{2}

也就是说，前向传播时，就是拿解码器输入 $z_{q} (x)$ 来算梯度。

L_{reconstruct} = ∥ x - decoder (z_{q} (x)) ∥_{2}^{2}

而反向传播时，按下面这个公式求梯度，等价于把解码器的梯度全部传给 $z_{e} (x)$ 。

L_{reconstruct} = ∥ x - decoder (z_{e} (x)) ∥_{2}^{2}

这部分的 PyTorch 实现如下所示。在 PyTorch 里，(x).detach() 就是 $s g (x)$ ，它的值在前向传播时取 $x$ ，反向传播时取 $0$ 。

1   L = x - decoder(z_e + (z_q - z_e).detach())

通过这一技巧，我们完成了梯度的传递，可以正常地训练编码器和解码器了。

优化嵌入空间

到目前为止，我们的讨论都是建立在嵌入空间已经训练完毕的前提上的。现在，我们来讨论一下嵌入空间的训练方法。

嵌入空间的优化目标是什么呢？嵌入空间的每一个向量应该能概括一类编码器输出的向量，比如一个表示「青年」的向量应该能概括所有 14–35 岁的人的照片的编码器输出。因此，嵌入空间的向量应该和其对应编码器输出尽可能接近。如下面的公式所示， $z_{e} (x)$ 是编码器的输出向量， $z_{q} (x)$ 是其在嵌入空间的最近邻向量。

L_{e} = ∥ z_{e} (x) - z_{q} (x) ∥_{2}^{2}

但作者认为，编码器和嵌入向量的学习速度应该不一样快。于是，他们再次使用了停止梯度的技术，把上面那个误差函数拆成了两部分。其中， $β$ 控制了编码器的相对学习速度。作者发现，算法对 $β$ 的变化不敏感， $β$ 取 0.1~2.0 都差不多。

L_{e} = ∥ s g (z_{e} (x)) - z_{q} (x) ∥_{2}^{2} + β ∥ z_{e} (x) - s g (z_{q} (x)) ∥_{2}^{2}

其实，在论文中，作者分别讨论了上面公式里的两个误差。第一个误差来自字典学习算法里的经典算法 Vector Quantisation (VQ)，也就是 VQ-VAE 里的那个 VQ，它用于优化嵌入空间。第二个误差叫做专注误差，它用于约束编码器的输出，不让它跑到离嵌入空间里的向量太远的地方。

这样，VQ-VAE 总体的损失函数可以写成：（由于算上了重建误差，我们多加一个 $α$ 用于控制不同误差之间的比例）

L = ∥ x - decoder (z_{e} (x) + s g (z_{q} (x) - z_{e} (x))) ∥_{2}^{2}

+ α ∥ s g (z_{e} (x)) - z_{q} (x) ∥_{2}^{2} + β ∥ z_{e} (x) - s g (z_{q} (x)) ∥_{2}^{2}

总结

VQ-VAE是一个把图像编码成离散向量的图像压缩模型。为了让神经网络理解离散编码，VQ-VAE借鉴了NLP的思想，让每个离散编码值对应一个嵌入，所有的嵌入都存储在一个嵌入空间（又称”codebook”）里。这样，VQ-VAE编码器的输出是若干个「假嵌入」，「假嵌入」会被替换成嵌入空间里最近的真嵌入，输入进解码器里。

VQ-VAE的优化目标由两部分组成：重建误差和嵌入空间误差。重建误差为输入图片和重建图片的均方误差。为了让梯度从解码器传到编码器，作者使用了一种巧妙的停止梯度算子，让正向传播和反向传播按照不同的方式计算。嵌入空间误差为嵌入和其对应的编码器输出的均方误差。为了让嵌入和编码器以不同的速度优化，作者再次使用了停止梯度算子，把嵌入的更新和编码器的更新分开计算。

训练完成后，为了实现随机图像生成，需要对VQ-VAE的离散分布采样，再把采样出来的离散向量对应的嵌入输入进解码器。VQ-VAE论文使用了PixelCNN来采样离散分布。实际上，PixelCNN不是唯一一种可用的拟合离散分布的模型。我们可以把它换成Transformer，甚至是diffusion模型。如果你当年看完VQ-VAE后立刻把PixelCNN换成了diffusion模型，那么恭喜你，你差不多提前设计出了Stable Diffusion。

可见，VQ-VAE最大的贡献是提供了一种图像压缩思路，把生成大图像的问题转换成了一个更简单的生成「小图像」的问题。图像压缩成离散向量时主要借助了嵌入空间，或者说”codebook”这一工具。这种解决问题的思路可以应用到所有图像生成类任务上，比如超分辨率、图像修复、图像去模糊等。所以近两年我们能看到很多使用了codebook的图像生成类工作。

代码实现

训练阶段

VQ-VAE 的训练阶段分为五个阶段:

我们将基于MINIST数据集进行训练演示

步骤 1️⃣：编码输入图像

用 Encoder 将输入图像 $x$ 编码为连续隐变量 $z_{e} (x)$ ，维度通常为 $[B, C, H, W]$ 。

这是一个普通的 CNN 编码过程，信息仍是连续的。

# =============================
# 编码器
# =============================
class Encoder(nn.Module):
    def __init__(self, in_channels=1, hidden_channels=128, z_channels=64):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels, hidden_channels, 4, stride=2, padding=1)  # 28x28 -> 14x14
        self.conv2 = nn.Conv2d(hidden_channels, z_channels, 4, stride=2, padding=1)   # 14x14 -> 7x7

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = self.conv2(x)
        return x

在 VQ-VAE 中，一张输入图像最终被编码为一个二维的“索引矩阵”，这个矩阵的每一个元素对应于 codebook 中的一个嵌入向量（embedding vector），表示该位置的图像特征。

不是编码为“一个嵌入向量”的原因

单一嵌入向量（如普通 VAE）：只能保留全局信息，比如图像的类别、姿态等，但无法表达空间结构。
二维嵌入索引矩阵：是每个图像区域（patch/block）对应一个离散 token，可保留局部+空间结构，适合还原复杂细节。

目标不同：压缩 vs 生成

传统 AE/VAE 通常用作图像压缩或聚类，输出一个固定维度的表示。
VQ-VAE 是为生成任务设计的：最终需要还原整张图像，因此不能只用一个全局向量（太少了），而必须保留空间布局。

步骤 2️⃣：量化连续隐变量（离散化）

将 $z_{e} (x)$ 中的每个空间位置的向量与 codebook 中的离散向量（embedding vectors）比较。
选取最相近的向量索引（最近邻搜索），即：
$z_{q} (x) = e_{k}, where k = \arg min_{j} ∥ z_{e} (x) - e_{j} ∥^{2}$
每个位置被替换为最接近的 codebook 向量，形成量化后的表示 $z_{q} (x)$ 。

# =============================
# 向量量化器
# =============================
class VectorQuantizer(nn.Module):
    def __init__(self, num_embeddings, embedding_dim, commitment_cost):
        super().__init__()
        self.embedding_dim = embedding_dim
        self.num_embeddings = num_embeddings
        self.beta = commitment_cost

        # 编码字典
        self.embedding = nn.Embedding(num_embeddings, embedding_dim)
        self.embedding.weight.data.uniform_(-1.0 / num_embeddings, 1.0 / num_embeddings)

    def forward(self, z):
        # z: [B, C, H, W]
        z_perm = z.permute(0, 2, 3, 1).contiguous()  # [B, H, W, C]
        z_flattened = z_perm.view(-1, self.embedding_dim)  # [BHW, C]

        # 欧氏距离计算
        dist = (
                torch.sum(z_flattened ** 2, dim=1, keepdim=True)
                - 2 * torch.matmul(z_flattened, self.embedding.weight.t())
                + torch.sum(self.embedding.weight ** 2, dim=1)
        )  # [BHW, num_embeddings]

        encoding_indices = torch.argmin(dist, dim=1)  # [BHW]
        quantized = self.embedding(encoding_indices)  # [BHW, C]

        # 恢复为 [B, H, W, C]
        quantized = quantized.view(z_perm.shape)  # [B, H, W, C]

        # 再 permute 回 [B, C, H, W]
        quantized = quantized.permute(0, 3, 1, 2).contiguous()

        # 向量量化损失
        e_latent_loss = F.mse_loss(quantized.detach(), z)  # <== 现在维度一致了
        q_latent_loss = F.mse_loss(quantized, z.detach())
        loss = q_latent_loss + self.beta * e_latent_loss

        # straight-through estimator
        quantized = z + (quantized - z).detach()
        
        encoding_indices = encoding_indices.view(z_perm.shape[0], z_perm.shape[1], z_perm.shape[2])  # [B, H, W]
        
        return quantized, loss, encoding_indices

步骤 3️⃣：解码离散表示

将 $z_{q} (x)$ 输入 Decoder，还原为重建图像 $\hat{x}$ 。
由于 Decoder 处理的是向量索引映射后的嵌入向量，仍然是连续空间中的解码。

# =============================
# 解码器
# =============================
class Decoder(nn.Module):
    def __init__(self, z_channels=64, hidden_channels=128, out_channels=1):
        super().__init__()
        self.conv1 = nn.ConvTranspose2d(z_channels, hidden_channels, 4, stride=2, padding=1)  # 7x7 -> 14x14
        self.conv2 = nn.ConvTranspose2d(hidden_channels, out_channels, 4, stride=2, padding=1)  # 14x14 -> 28x28

    def forward(self, z):
        z = F.relu(self.conv1(z))
        z = torch.sigmoid(self.conv2(z))
        return z

步骤 4️⃣：计算损失函数（包括三项）

总损失由三个部分组成：

重建误差（图像像素级别 MSE 或 BCE）：
$L_{recon} = ∥ x - \hat{x} ∥^{2}$
codebook 损失（VQ loss）：鼓励 codebook 向量靠近 encoder 输出：
$L_{codebook} = ∥ sg [z_{e} (x)] - e ∥^{2}$
承诺损失（commitment loss）：鼓励 encoder 输出靠近 codebook 向量：
$L_{commit} = β \cdot ∥ z_{e} (x) - sg [e] ∥^{2}$
其中 $sg [\cdot]$ 表示 stop gradient，防止梯度传播到某部分。

总损失为：

L = L_{recon} + L_{codebook} + L_{commit}

# =============================
# VQ-VAE 组合模型
# =============================
class VQVAE(nn.Module):
    def __init__(self, in_channels=1, z_channels=64, num_embeddings=512, commitment_cost=0.25):
        super().__init__()
        self.encoder = Encoder(in_channels, z_channels=z_channels)
        self.vq = VectorQuantizer(num_embeddings, z_channels, commitment_cost)
        self.decoder = Decoder(z_channels)

    def forward(self, x):
        z = self.encoder(x)
        quantized, vq_loss, encoding_indices = self.vq(z)
        x_recon = self.decoder(quantized)
        return x_recon, vq_loss, encoding_indices

步骤 5️⃣：反向传播与参数更新

使用 straight-through estimator（STE）将编码器的梯度绕过非可导的 nearest neighbor 操作，近似回传。
三部分参数更新：
- Encoder 更新：通过 STE 反向传播 $z_{q}$ 的损失；
- Codebook 更新：更新嵌入向量（支持 EMA 或普通梯度更新）；
- Decoder 更新：通过正常反向传播重建误差更新。

# 加载数据集
transform = transforms.Compose([transforms.ToTensor()])
train_dataset = torchvision.datasets.MNIST(root='./data', train=True, transform=transform, download=True)
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)

# 初始化模型
model = VQVAE().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

# 加载预训练模型（可选）
model_loaded = False
try:
    model.load_state_dict(torch.load("vqvae.pth", map_location=device))
    print("✅ 成功加载预训练的 VQ-VAE 模型权重")
    model_loaded = True
except FileNotFoundError:
    print("⚠️ 未找到预训练模型，开始从头训练")


# 训练模型
if not model_loaded:
    num_epochs = 10
    for epoch in range(num_epochs):
        model.train()
        total_recon_loss = 0
        total_vq_loss = 0
        for x, _ in train_loader:
            x = x.to(device)
            x_recon, vq_loss, _ = model(x)
            recon_loss = F.mse_loss(x_recon, x)
            loss = recon_loss + vq_loss

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            total_recon_loss += recon_loss.item()
            total_vq_loss += vq_loss.item()

        print(f"Epoch [{epoch+1}/{num_epochs}], Recon Loss: {total_recon_loss:.4f}, VQ Loss: {total_vq_loss:.4f}")
    # 保存模型
    torch.save(model.state_dict(), "vqvae.pth")
else:
    print("⏭️ 已加载预训练模型，跳过训练过程")

生成阶段

VQ-VAE：学习将图像压缩为离散 latent 表示，并能重建图像。
PixelCNN：学习这些离散 latent 的分布，从而生成新的 latent 表示。
解码阶段：用训练好的 VQ-VAE decoder，将 PixelCNN 采样的 latent 转换为图像。

PixelCNN 模型实现如下(只有空间掩码卷积):

class MaskedConv2d(nn.Conv2d):
    def __init__(self, mask_type, *args, **kwargs):
        super().__init__(*args, **kwargs)
        assert mask_type in ['A', 'B']
        self.mask_type = mask_type
        self.register_buffer('mask', torch.ones_like(self.weight))

        _, _, h, w = self.weight.size()
        yc, xc = h // 2, w // 2

        self.mask[:, :, yc, xc+1:] = 0
        self.mask[:, :, yc+1:] = 0
        if mask_type == 'A':
            self.mask[:, :, yc, xc] = 0

    def forward(self, x):
        self.weight.data *= self.mask
        return super().forward(x)

class PixelCNN(nn.Module):
    def __init__(self, num_embeddings, in_channels=1, hidden_channels=64, num_layers=7):
        super().__init__()
        layers = [MaskedConv2d('A', in_channels, hidden_channels, kernel_size=7, padding=3), nn.ReLU()]
        for _ in range(num_layers - 2):
            layers.append(MaskedConv2d('B', hidden_channels, hidden_channels, 3, padding=1))
            layers.append(nn.ReLU())
        layers.append(nn.Conv2d(hidden_channels, num_embeddings, 1))
        self.net = nn.Sequential(*layers)

    def forward(self, x):
        return self.net(x)

基于已经训练好的VQ-VAE模型，再次扫描训练集，提取训练集中每个图像对应的离散 latent 索引列表

# 假设：vqvae = VQVAE(...)，已经训练完毕或已加载权重
# 使用训练集提取离散 latent 索引
model.eval()
all_indices = []

with torch.no_grad():
    for img, _ in train_loader:
        z_e = model.encoder(img.to(device))
        _, _, indices = model.vq(z_e)
        all_indices.append(indices.cpu())

# 拼接为 [B , H , W]
all_indices = torch.cat(all_indices, dim=0)

基于离散 latent 索引列表，训练 PixelCNN 模型，学习这些离散 latent 的分布规律：

# PixelCNN 训练（学习 latent 索引分布）
pixelcnn = PixelCNN(num_embeddings=512).to(device)
optimizer = torch.optim.Adam(pixelcnn.parameters(), lr=1e-3)
loss_fn = nn.CrossEntropyLoss()

# 加载预训练 PixelCNN 模型（可选）
pixelcnn_loaded = False
try:
    pixelcnn.load_state_dict(torch.load("pixelcnn.pth", map_location=device))
    print("✅ 成功加载预训练的 PixelCNN 模型权重")
    pixelcnn_loaded = True
except FileNotFoundError:
    print("⚠️ 未找到预训练 PixelCNN 模型，开始从头训练")

if not pixelcnn_loaded:
    for epoch in range(10):
        total_loss = 0
        for i in range(0, all_indices.size(0), 64):
            batch = all_indices[i:i+64].to(device)
            input = batch.unsqueeze(1).float()
            target = batch.long()
            
            # input 维度: (64,1,7,7) , logits 维度: (64,512,7,7) ，target 维度: (64,7,7)
            logits = pixelcnn(input)
            loss = loss_fn(logits, target)

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            total_loss += loss.item()

        print(f"[PixelCNN] Epoch {epoch+1} Loss: {total_loss:.4f}")
    # 保存模型
    torch.save(pixelcnn.state_dict(), "pixelcnn.pth")
else:
    print("⏭️ 已加载预训练 PixelCNN 模型，跳过训练过程")

PixelCNN 学习的是 latent index 的分布

PixelCNN 生成 latent 索引 → VQ-VAE 解码成图像

def sample_latent(pixelcnn, shape, num_embeddings):
    pixelcnn.eval()
    with torch.no_grad():
        B, H, W = shape
        sample = torch.zeros((B, 1, H, W)).to(device)  # 初始化 sample
        for i in range(H):
            for j in range(W):
                logits = pixelcnn(sample)
                probs = F.softmax(logits[:, :, i, j], dim=-1)
                sample[:, 0, i, j] = torch.multinomial(probs, 1).squeeze(-1)
        return sample.squeeze(1).long()  # [B, H, W]

# 从 PixelCNN 生成 latent 索引
sampled_indices = sample_latent(pixelcnn, shape=(8, 7, 7), num_embeddings=512)

# 还原为 codebook 嵌入向量
embeddings = model.vq.embedding.weight
quantized = embeddings[sampled_indices.view(-1)].view(8, 7, 7, -1).permute(0, 3, 1, 2).contiguous()

# 解码成图像
with torch.no_grad():
    recon = model.decoder(quantized).cpu()

# 可视化
import matplotlib.pyplot as plt
for i in range(8):
    plt.subplot(2, 4, i+1)
    plt.imshow(recon[i][0], cmap='gray')
    plt.axis('off')
plt.suptitle("Generated Images from PixelCNN + VQ-VAE")
plt.show()

由于训练轮次很少，所以效果也比较差:

转载

本文转载至: 轻松理解 VQ-VAE：首个提出 codebook 机制的生成模型