Unsupervised Label Noise Modeling and Loss Correction 论文

BinaryOracle2025/9/18大约 42 分钟约 12666 字

Unsupervised Label Noise Modeling and Loss Correction 论文

论文链接: Unsupervised Label Noise Modeling and Loss Correction
代码链接: https://github.com/PaulAlbert31/LabelNoiseCorrection

引言

卷积神经网络（CNN）是计算机视觉任务中的主流方法，能够在有大量标注数据时建模复杂模式。但实际中获取大规模干净数据很困难，人工或自动标注往往会产生错误，形成噪声样本。

已有研究发现：

CNN 虽然对少量噪声有一定鲁棒性，但在随机梯度下降训练下，容易 拟合随机标签。
当同时存在干净和错误标签时，网络会先拟合干净样本，再逐步拟合噪声样本。
过拟合噪声会严重损害模型的泛化能力，也会加剧训练中的偏差问题（如类别不平衡）。

因此，如何在不丢弃噪声样本的前提下，避免网络过拟合错误标签，同时利用这些样本的潜在信息，成为一个关键挑战。

现有方法与不足：

损失校正类方法：
- Bootstrapping loss（Reed 等, 2015）在目标函数中引入一致性约束，通过结合网络预测结果和原始标签，减少噪声的负面影响。
- 类别概率修正（Patrini 等, 2017; Hendrycks 等, 2018）通过估计每类的噪声分布，对损失进行调整，引导网络更靠近真实类别。
课程学习类方法：
- 通过“由易到难”的顺序训练（Bengio 等, 2009），在噪声场景中，易样本≈干净样本，难样本≈噪声样本，因此可以降低噪声样本对损失的贡献。
- 但简单丢弃噪声样本可能损失了关于数据分布的重要信息。
其他改进方法：
- 相似性学习（Wang 等, 2018b）：将噪声样本的表示与干净样本拉开。
- Mixup 数据增强（Zhang 等, 2018）：无需显式建模噪声，却展现出对标签噪声的强鲁棒性。

然而，这些方法往往假设存在一部分干净数据，或者在利用噪声样本方面不够充分。

本文的核心思想与贡献：

本文提出一种新的训练流程，即使在高比例噪声下，也能避免过拟合错误标签，同时有效利用噪声样本：

通过对 样本损失分布 进行建模，提出 双成分 Beta 混合模型 (BMM)，分别对应“干净样本”和“噪声样本”。
使用 BMM 的后验概率来动态调整 bootstrapping loss，从而实现对每个样本的损失校正。
在不丢弃噪声样本的情况下，保持训练鲁棒性，并能学习到有利的表征。
将方法与 mixup 数据增强 结合，进一步提升性能，即便在极端噪声条件下依然能收敛。

主要贡献：

提出基于样本损失的无监督标签噪声建模方法。
提出结合该模型的损失校正策略，避免过拟合噪声标签。
将方法与 mixup 数据增强结合，推动了当前最优水平的提升。
在极端噪声水平下，依然能通过改进的 mixup 策略实现收敛。

方法

1. 标签噪声建模

图像分类被定义为从训练集

$D = {(x_{i}, y_{i})}_{i = 1}^{N}$

学习一个模型 $h_{θ} (x)$ ，其中 $y_{i}$ 是 one-hot 标签。本文中 $h_{θ}$ 是 CNN， $θ$ 是权重和偏置。训练通过最小化交叉熵损失：

L (θ) = - \sum_{i = 1}^{N} y_{i}^{T} \log (h_{θ} (x_{i})) .

当标签含有噪声时，样本 $x_{i}$ 可能带有错误标签，因此需要扩展损失函数来抵抗噪声。

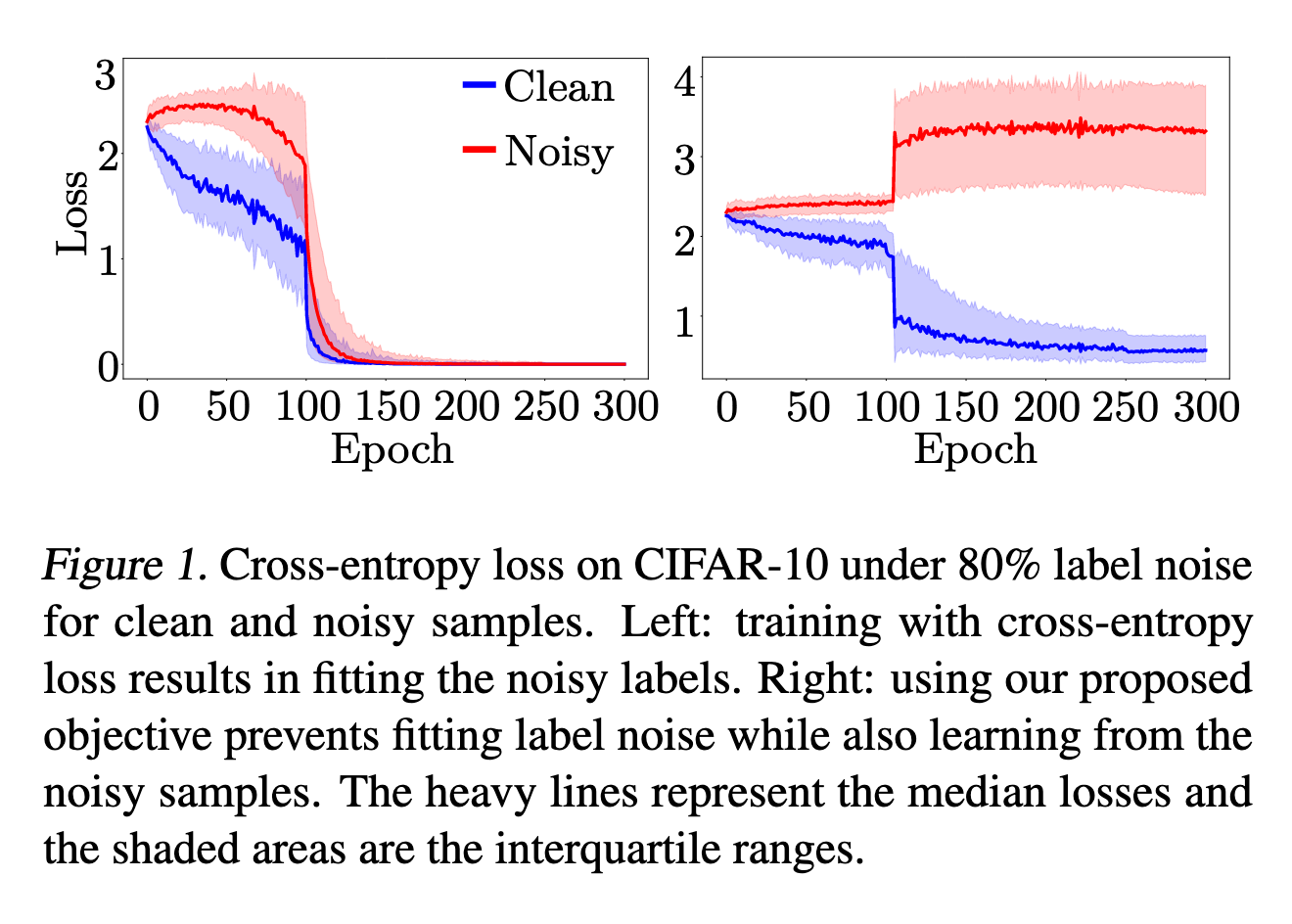
核心观察（见图1与图2）：

随机错误标签比正确标签更难学，因此在训练早期，噪声样本的损失值更高。
CNN 在拟合干净样本后才逐渐拟合噪声样本。
因此，仅通过损失分布就能区分干净与噪声样本。

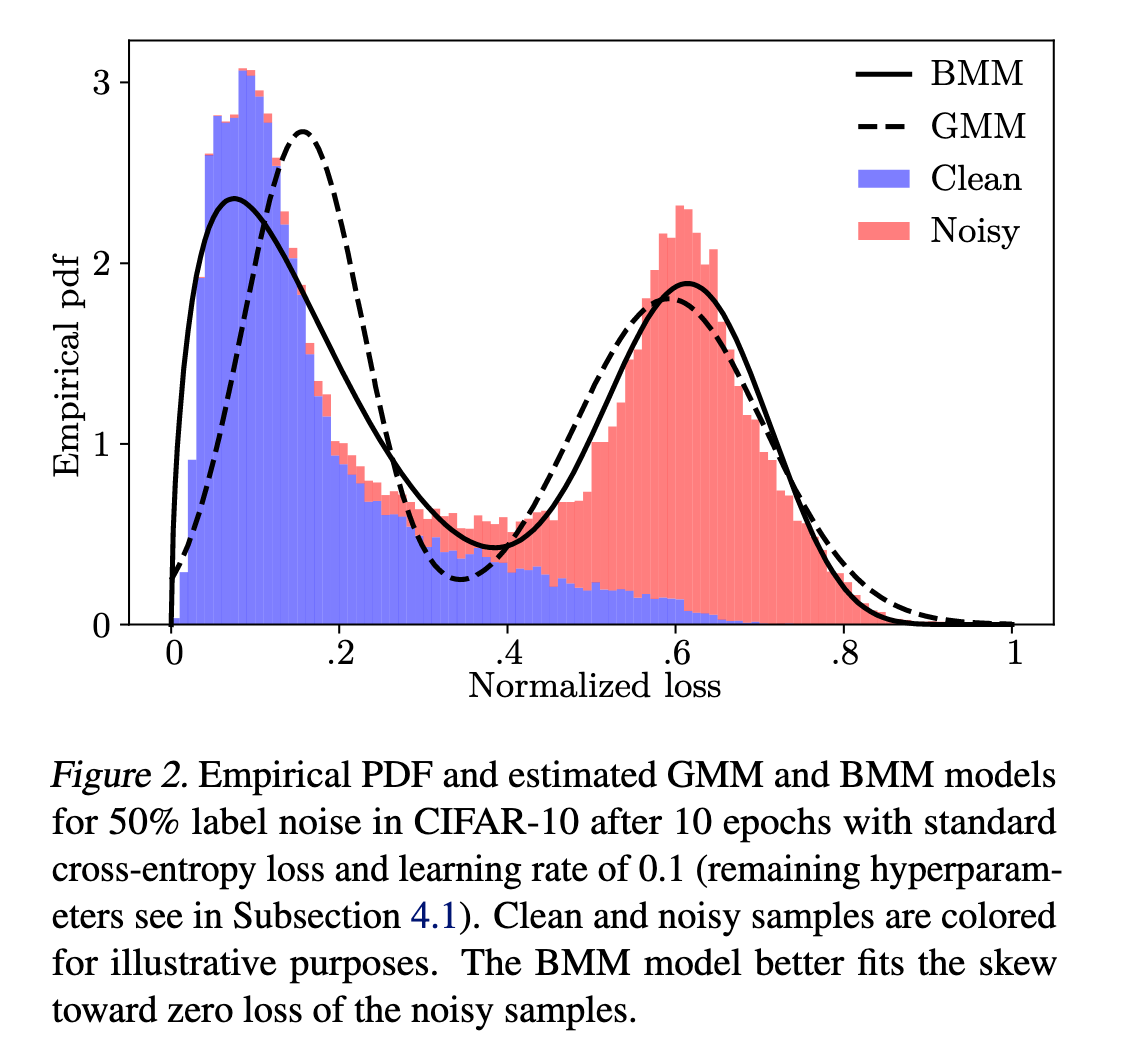
这启发了本文提出的：通过 混合模型 对损失分布建模，进而判别样本是否为噪声。

混合模型的选择：

一般混合模型定义为：
$p (L) = \sum_{k = 1}^{K} λ_{k} p (L ∣ k),$
其中 $λ_{k}$ 是混合系数。
直观做法是使用 高斯混合模型(GMM) 来区分干净与噪声（ $K = 2$ ）。
但高斯分布不能很好刻画干净样本的分布，因为其损失高度偏向零。
Beta 分布 更灵活，能拟合 $[0, 1]$ 区间的对称或偏态分布，因此 Beta 混合模型(BMM) 更适合。
实验表明：在 CIFAR-10 上 80% 标签噪声条件下，BMM 相比 GMM 在 ROC-AUC 提升约 5 个点（见附录A）。

Beta 分布定义：

p (L ∣ α, β) = \frac{Γ (α + β)}{Γ (α) Γ (β)} L^{α - 1} (1 - L)^{β - 1}, α, β > 0

将其代入公式(2)，即可得到 BMM 的概率密度函数。

参数估计：EM 算法流程

E 步（公式(4)）：固定参数，计算后验概率 $γ_{k} (L)$ ，即样本损失来自分量 $k$ 的概率。
M 步（公式(5)(6)(7)）：根据加权矩方法更新 $α_{k}, β_{k}$ ，并计算加权均值 ${\bar{L}}_{k}$ 与方差 $s_{k}^{2}$ 。
更新混合系数（公式(8)）：
$λ_{k} = \frac{1}{N} \sum_{i = 1}^{N} γ_{k} (L_{i})$
交替进行 E/M 步，直至收敛或迭代 10 次（本文实验设置）。
数值稳定性处理：为避免 $L \approx 0$ 或 $L \approx 1$ 导致的不稳定，作者将观测值限制在区间 $[ϵ, 1 - ϵ]$ ，其中 $ϵ = 10^{- 4}$ 。

最终判别结果（公式(9)）：

得到样本为干净或噪声的概率：
$p (k ∣ L_{i}) = \frac{p (k) p (L_{i} ∣ k)}{p (L_{i})}, k = 0, 1$
$k = 0$ 表示干净样本， $k = 1$ 表示噪声样本。
用于估计分布的损失始终是 标准交叉熵损失，在每个 epoch 后对所有样本重新计算。这与训练损失可能不同，因为训练时会引入噪声修正项。

2. 用于标签修正的噪声模型总结

在存在标签噪声的情况下，选择合适的损失函数对学习过程非常关键。标准的分类交叉熵损失（见公式 (1)）并不适合，因为它会让模型去拟合噪声标签（Zhang 等，2017）。

Reed 等（2015）提出了 静态硬自举损失（static hard bootstrapping）。这种方法在标准交叉熵中加入了一个感知项，用来修正训练目标。其定义为：

B = - \sum_{i = 1}^{N} ((1 - w_{i}) y_{i} + w_{i} z_{i})^{T} \log (h_{i})

其中， $w_{i}$ 控制模型预测 $z_{i}$ 在损失中的权重。Reed 等人设定 $w_{i} = 0.2, \forall i$ 。在这种情况下，样本的真实标签 $y_{i}$ 占主要部分，但模型预测 $z_{i}$ 也会有一定影响。

他们还提出了 静态软自举损失（static soft bootstrapping），将预测的 softmax 概率 $h_{i}$ 代替 $z_{i}$ ，并固定 $w_{i} = 0.05, \forall i$ 。这意味着更多依赖标签 $y_{i}$ ，但依然引入了一点模型预测的作用。

然而，固定权重的方式存在两个问题（如第 4.2 小节表 1 所示）：

它不能阻止模型去拟合噪声样本。
当 $w_{i}$ 过小且固定时，对潜在噪声标签 $y_{i}$ 的修正能力受到限制。

为了解决这些问题，本文提出了 动态硬自举 和 动态软自举 方法。它们的关键是使用噪声模型对每个样本单独加权，即动态地设定 $w_{i} = p (k = 1 ∣ ℓ_{i})$ ，其中 $ℓ_{i}$ 是样本的交叉熵损失。BMM（Beta Mixture Model）会在每个训练轮次后基于 $ℓ_{i}$ 进行重新估计。

这样一来：

对于干净样本， $1 - w_{i}$ 较大，因此损失主要依赖真实标签 $y_{i}$ 。
对于噪声样本， $w_{i}$ 较大，因此损失主要由类别预测 $z_{i}$ 或概率预测 $h_{i}$ 主导，分别对应动态硬自举与动态软自举。

$z_{i}$ 是 $o n e h o t$ 标签，而 $h_{i}$ 是 $s o f t m a x$ 输出的概率分布。

在训练后期，CNN 模型能够更好地估计噪声样本的真实类别，因此这种方法更有效。第 4.2 小节的实验表明：动态自举在效果上明显优于静态自举。

3. 联合标签修正与 mixup 数据增强

mixup 数据增强方法（Zhang 等，2018）通过对样本对 $(x_{p}, x_{q})$ 和标签对 $(y_{p}, y_{q})$ 做凸组合来训练网络：

x = δ x_{p} + (1 - δ) x_{q}, ℓ = δ ℓ_{p} + (1 - δ) ℓ_{q}

其中 $δ$ 从 Beta 分布 $B e (α, β)$ 中采样。处理标签噪声时，通常将 $α = β$ 设置较大，使 $δ$ 接近 0.5。这样网络在训练样本之间保持线性行为，减少远离训练样本区域的输出波动。mixup 还能结合干净样本与噪声样本，计算更具代表性的损失，即使组合的是两个噪声样本，计算的损失也可能有用，因为其中一个样本可能偶然包含另一个样本的真实标签。mixup 有助于模型学习有结构的数据，同时抑制无结构噪声的影响。

为了进一步提高鲁棒性，本文提出将 mixup 与动态自举（dynamic bootstrapping）结合，实现针对每个样本的损失修正：

ℓ^{*} = - δ [((1 - w_{p}) y_{p} + w_{p} z_{p})^{T} \log (h)] - (1 - δ) [((1 - w_{q}) y_{q} + w_{q} z_{q})^{T} \log (h)]

$ℓ^{*}$ 为硬自举版本，软自举版本通过将 $z_{p}$ 和 $z_{q}$ 替换为 $h_{p}$ 和 $h_{q}$ 定义。
权重 $w_{p}$ 和 $w_{q}$ 由无监督噪声模型推断得到：

w_{p} = p (k = 1 ∣ ℓ_{p}), w_{q} = p (k = 1 ∣ ℓ_{q})

为了获取 $h_{p}, z_{p}, h_{q}, z_{q}$ ，需要额外前向传播，因为混合后的概率 $h$ 无法直接得到样本 $p$ 和 $q$ 的预测。

该方法利用 mixup 的优势，同时通过动态自举对标签进行修正。在训练过程中，随着预测逐步改进， $ℓ^{*}$ 有助于模型学习更好结果。然而，在高噪声水平下，网络预测不可靠，动态自举可能不收敛，因为大多数样本在自举损失中被网络预测主导，这可能导致网络倾向预测同一类别以最小化损失。

如果大多数样本的损失都被网络预测主导，模型会发现一个“捷径”——总是预测同一个类别可以让损失最小。

为解决高噪声问题，本文引入 Tanaka 等（2018）提出的正则项，防止模型将所有样本分配到同一类别：

R = \sum_{c = 1}^{C} p_{c} \log (\frac{p_{c}}{h_{c}})

$p_{c}$ 为类别 $c$ 的先验概率（假设均匀分布 $p_{c} = 1 / C$ ）
$h_{c}$ 为模型在整个数据集上类别 $c$ 的平均 softmax 概率（通过 mini-batch 近似计算）

最终将正则项加权系数 $η$ 加入 $ℓ^{*}$ 中（公式 (13)），在实验中 $η = 1$ 。第 4.3 小节展示了该方法效果，第 4.5 小节表明其性能优于现有最先进方法。

KL散度约束: 惩罚模型把所有样本预测成同一类别的行为; 鼓励模型输出各类别概率尽量接近均匀分布; 在高噪声情况下，避免动态自举引导模型陷入“单一类别捷径”。

实验

1. 静态与动态自举

动态自举（DY）总体优于静态自举（ST），尤其在高噪声下表现更明显（80%标签噪声下，DY-H 64.2% vs ST-H 25.7%）。
硬自举（Hard）效果优于软自举（Soft），符合 Reed 等（2015）的结论。
使用每样本权重（动态自举）有助于充分修正噪声标签，提高模型在噪声数据下的训练效果。

2. 联合 mixup 与动态自举

动态硬自举比静态方法更优，但单独 mixup 数据增强在高噪声下仍表现优秀。
将动态自举的每样本加权与 mixup 结合（M-DYR-H 和 M-DYRS），在高噪声下显著提升准确率（表2）。
结合方法在 80% 标签噪声下超过单独 mixup 的性能，说明融合策略兼顾了噪声修正与正则化能力。

3. 极端噪声（90%标签噪声）

M-DYR-H 在 CIFAR-10 90%标签噪声下无法收敛。
采用动态 mixup（不同 δ 指导混合比例）和递减 softmax 温度策略（MD-DYR-H / MD-DYR-SH）可稳定训练并提升性能。
MD-DYR-SH 在 CIFAR-10 90%噪声下达 69.1%，CIFAR-100 24.3%，远超现有方法（Tanaka 等 2018 最佳 58.3%）。

4. 与现有方法对比

在 80%-90%标签噪声下，本文方法显著优于 Reed（2015）、Patrini（2017）及 mixup（Zhang 等 2018）；
在随机标签不保留真实标签的情况下（Jiang 等, 2018b），MD-DYR-SH 依然优于现有方法，M-DYR-H 在低噪声下略逊于 Jiang 等，但整体表现仍优秀；
高噪声下现有方法难以有效利用噪声样本，容易过拟合噪声标签。

5. 泛化性

在 TinyImageNet 上，MDYR-H 和 MD-DYR-SH 超过 mixup，在不同噪声水平下表现稳定；
在真实世界标签噪声数据 Clothing1M 上，使用 ResNet-50 预训练网络测试准确率 71%，略低于最先进方法 72.23%，说明方法在实际噪声场景下仍有优势，但受预训练和微调策略影响。

总体结论：

动态自举 + mixup 的组合策略（M-DYR-H / MD-DYR-SH）在高噪声数据上效果最优；
硬自举适用于中低噪声，但在极高噪声下需结合温度衰减和动态 mixup 才能稳定训练；
方法在 CIFAR、TinyImageNet 和 Clothing1M 上均显示良好的泛化能力。

结论

本文提出了一种在标签噪声下训练 CNN 的新方法，该方法不依赖任何干净数据集。我们通过对每个样本的交叉熵损失拟合 Beta 混合模型，以无监督方式建模标签噪声。基于该模型，我们实现了一种动态自举损失，该损失根据混合模型的结果，在网络预测值或真实标签（可能含噪声）之间选择使用。

此外，我们将动态自举与 mixup 数据增强相结合，实现了一种极其鲁棒的损失修正方法。在 CIFAR-10 和 CIFAR-100 上进行了大量实验，验证了方法的优缺点，并展示了卓越的性能。我们进一步提出利用 Beta 混合模型指导 mixup 数据增强的组合，以确保在极端噪声水平下训练的可靠收敛。

该方法在 TinyImageNet 上表现出良好的泛化能力，但在 Clothing1M 的非均匀噪声情况下存在一些局限性，这将在未来研究中进一步探索。

代码实现

期望最大化（Expectation-Maximization, EM）算法

EM 是一种处理“隐藏变量”或不完全数据”的参数估计方法。

问题：你有观测数据 $X = {x_{1}, x_{2}, . . ., x_{N}}$ ，但模型中存在隐藏变量 $Z = {z_{1}, . . ., z_{N}}$ （比如样本属于哪个分量）
目标：估计模型参数 $θ$ （例如 Beta 分布的 $α, β$ 和混合权重 $π$ ）
难点：直接最大化似然函数很困难，因为隐藏变量未知

EM 的核心思想：

交替做两件事：
E-step：根据当前参数估计隐藏变量的分布（“猜测每个样本属于哪个分量”）
M-step：在隐藏变量已知的假设下，更新参数，使似然最大（用“责任”加权更新参数）
EM 算法就是解决“已知数据分布形式，但部分信息（隐藏变量）未知”的参数估计问题。它通过 交替猜测隐藏变量 → 根据猜测更新参数 的方式逼近最大似然估计。

论文中所提供的 EM 算法整体流程框架如下:

def fit(self, x):
    # 拷贝输入数据，避免修改原始数组 (输入的是每个样本的损失值)
    x = np.copy(x)

    # ----------------------------
    # 对数据做数值修正，保证 Beta 分布计算稳定
    # Beta 分布定义在开区间 (0, 1)，x=0 或 x=1 会导致 pdf 或矩估计出现数值不稳定
    # eps 用来把 0/1 附近的值略微拉开
    # ----------------------------
    eps = 1e-4
    x[x >= 1 - eps] = 1 - eps  # 将大于等于 1-eps 的值置为 1-eps
    x[x <= eps] = eps          # 将小于等于 eps 的值置为 eps

    # ----------------------------
    # 开始 EM 迭代
    # ----------------------------
    for i in range(self.max_iters):
        # ------------------------
        # E-step（期望步）
        # 计算每个样本属于每个 Beta 分量的责任
        # r.shape = (2, N)，r[k, i] 表示第 i 个样本属于分量 k 的概率
        # ------------------------
        r = self.responsibilities(x)

        # ------------------------
        # M-step（最大化步）
        # 使用责任 r 对每个分量的 Beta 分布参数进行加权拟合
        # fit_beta_weighted 使用加权矩估计得到 alpha 和 beta
        # ------------------------
        self.alphas[0], self.betas[0] = fit_beta_weighted(x, r[0])  # 更新第 0 个分量
        self.alphas[1], self.betas[1] = fit_beta_weighted(x, r[1])  # 更新第 1 个分量

        # ------------------------
        # 更新混合权重 pi_k
        # 根据责任求每个分量的总权重，然后归一化
        # ------------------------
        self.weight = r.sum(axis=1)       # 每个分量的总责任
        self.weight /= self.weight.sum()  # 归一化，使 sum(weight)=1

    # 返回训练好的模型实例
    return self

1. E-step（期望步）: 作者使用两个混合 Beta 分布分别建模干净样本和噪声样本的损失分布。在 E 步中，首先根据当前模型参数，计算每个样本属于 Beta1（干净样本损失分布）和 Beta2（噪声样本损失分布）的后验概率（responsibility），即每个样本属于各分量的概率，这两个概率经过归一化保证和为 1。

def likelihood(self, x, y):
    """
    计算样本 x 在第 y 个 Beta 分量下的似然（概率密度函数值）
    
    参数:
        x : array-like
            样本数据，可以是单个值或向量
        y : int
            分量索引，0 表示 Beta1，1 表示 Beta2
    
    返回:
        array-like
            样本 x 在 Beta 分布 y 下的概率密度
    """
    return stats.beta.pdf(x, self.alphas[y], self.betas[y])


def weighted_likelihood(self, x, y):
    """
    计算样本 x 在第 y 个 Beta 分量下的加权似然
    
    参数:
        x : array-like
            样本数据
        y : int
            分量索引
    
    返回:
        array-like
            样本 x 在 Beta 分量 y 下的加权概率密度，即 pdf * 分量权重
    """
    # self.weight[y] 是当前 Beta 分量的混合权重 π_y
    return self.weight[y] * self.likelihood(x, y)


def responsibilities(self, x):
    """
    E-step 的核心：计算每个样本属于各个 Beta 分量的后验概率（responsibility）
    
    参数:
        x : array-like
            样本数据
    
    返回:
        r : ndarray, shape=(2, N)
            r[k, i] 表示样本 i 属于分量 k 的概率
    """
    # 先计算每个样本在各个分量下的加权似然
    # r.shape = (2, N)，每行对应一个分量，每列对应一个样本
    r = np.array([self.weighted_likelihood(x, i) for i in range(2)])
    
    # 防止数值过小导致除零或 NaN
    # 将小于 eps_nan 的概率置为 eps_nan
    r[r <= self.eps_nan] = self.eps_nan
    
    # 对每个样本归一化，使两行（两个分量）概率和为 1
    # 对应公式: r_{ik} = π_k * pdf(x_i | θ_k) / sum_j(π_j * pdf(x_i | θ_j))
    r /= r.sum(axis=0)
    
    return r

2. M-step（最大化步）: 利用 E 步得到的责任（作为权重），对每个分量重新估计参数。

def weighted_mean(x, w):
    """
    计算加权平均值
    
    参数:
        x : array-like
            样本数据
        w : array-like
            权重向量，对应每个样本的权重（例如 EM 算法中的责任 r）
    
    返回:
        float
            加权平均值
    """
    # 加权平均值公式：sum(w_i * x_i) / sum(w_i)
    return np.sum(w * x) / np.sum(w)


def fit_beta_weighted(x, w):
    """
    根据加权样本估计 Beta 分布的参数 alpha 和 beta
    
    参数:
        x : array-like
            样本数据，取值范围应在 (0, 1)
        w : array-like
            权重向量，用于加权估计（例如来自 E-step 的责任）
    
    返回:
        (alpha, beta) : tuple of floats
            拟合得到的 Beta 分布参数
    """
    # Step 1: 计算加权均值
    x_bar = weighted_mean(x, w)  
    
    # Step 2: 计算加权方差
    s2 = weighted_mean((x - x_bar)**2, w)
    
    # Step 3: 根据矩估计公式推导 alpha
    # Beta 分布的均值 mu = alpha / (alpha + beta)
    # 方差 sigma^2 = alpha*beta / ((alpha+beta)^2 * (alpha+beta+1))
    # 通过加权均值和方差反解得到 alpha
    alpha = x_bar * ((x_bar * (1 - x_bar)) / s2 - 1)
    
    # Step 4: 根据均值公式反解 beta
    beta = alpha * (1 - x_bar) / x_bar
    
    # 返回估计的参数
    return alpha, beta

加权平均值公式: 在计算平均时考虑“重要性”，权重越大，样本对结果的影响越大; 对比普通求平均值，所有样本的权重都是 $1 / N$ 。

加权方差公式: 加权方差考虑了样本的“重要性”，权重越大的样本，其“离均值的偏差”对整体方差的贡献更大。

完整的EM算法执行过程如下图所示:

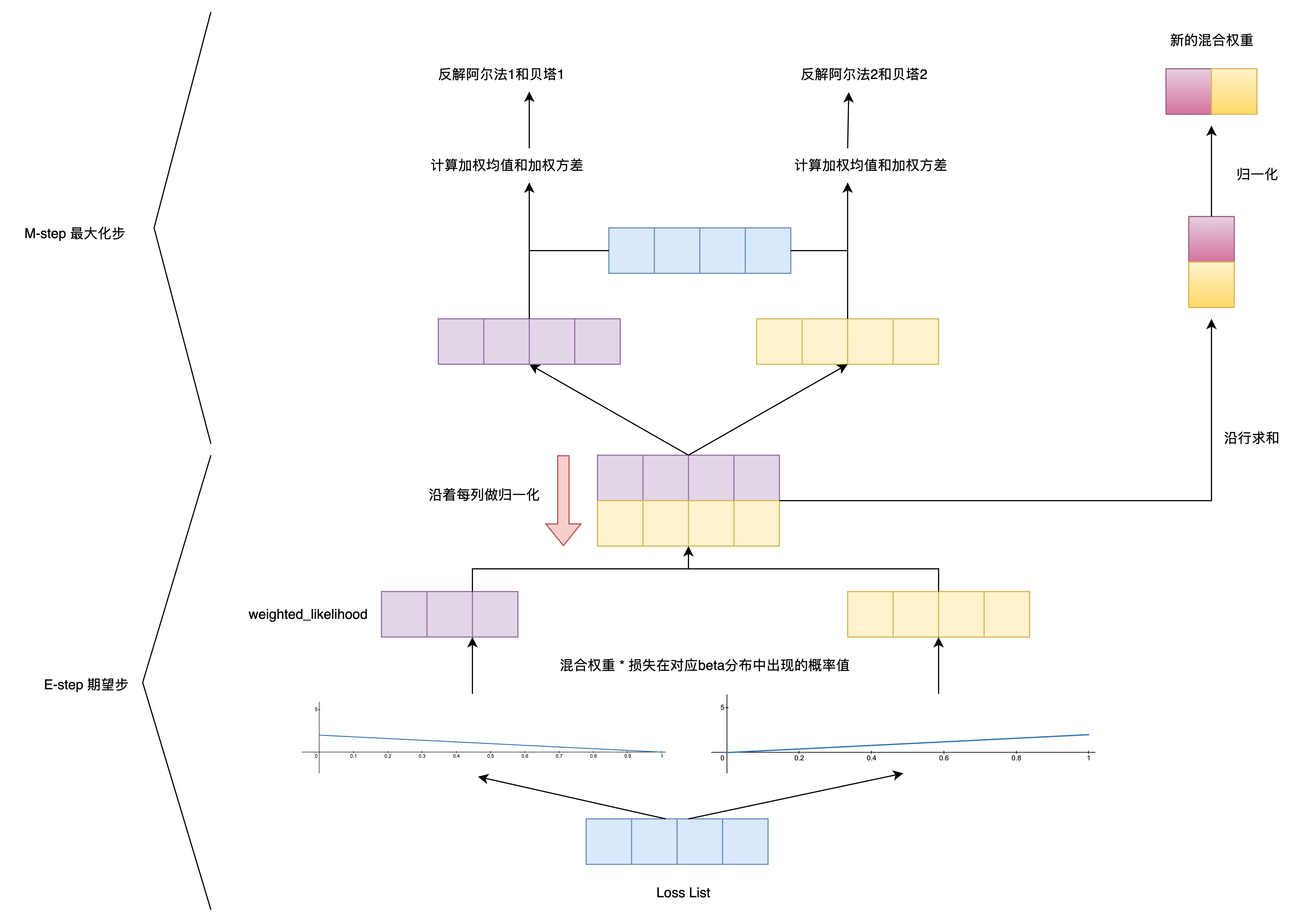
标签噪声建模

def track_training_loss(args, model, device, train_loader, epoch, bmm_model1, bmm_model_maxLoss1, bmm_model_minLoss1):
    '''
    跟踪训练集上的每个样本损失，并拟合 Beta 混合模型（BMM）用于噪声样本检测。
    
    输入:
    - args: 一些训练参数（未在函数内部使用）
    - model: 当前训练的神经网络模型
    - device: 'cuda' 或 'cpu'
    - train_loader: 训练数据加载器
    - epoch: 当前训练轮数
    - bmm_model1, bmm_model_maxLoss1, bmm_model_minLoss1: 之前轮次的 BMM 模型及最大/最小损失
    
    输出:
    - all_losses: 每个样本的 NLL 损失
    - all_probs: 每个样本的 log_softmax 概率
    - all_argmaxXentropy: 基于预测类别的交叉熵损失
    - bmm_model: 拟合当前 epoch 的 Beta 混合模型
    - bmm_model_maxLoss: 当前 epoch 的最大损失值（用于归一化）
    - bmm_model_minLoss: 当前 epoch 的最小损失值（用于归一化）
    '''
    
    # 设置模型为评估模式，不计算梯度
    model.eval()

    # 用于存储全量样本信息
    all_losses = torch.Tensor()
    all_predictions = torch.Tensor()
    all_probs = torch.Tensor()
    all_argmaxXentropy = torch.Tensor()

    # 遍历训练集 batch
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        prediction = model(data)  # 前向预测

        # 1. 对预测值做 log_softmax
        prediction = F.log_softmax(prediction, dim=1)

        # 2. 计算每个样本的负对数似然损失（NLL）
        idx_loss = F.nll_loss(prediction, target, reduction='none')
        idx_loss.detach_()  # 不计算梯度
        all_losses = torch.cat((all_losses, idx_loss.cpu()))  # 收集到全量损失

        # 3. 保存概率信息
        probs = prediction.clone()
        probs.detach_()
        all_probs = torch.cat((all_probs, probs.cpu()))

        # 4. 基于预测类别的交叉熵
        arg_entr = torch.max(prediction, dim=1)[1]  # 取预测最大值类别索引
        arg_entr = F.nll_loss(prediction.float(), arg_entr.to(device), reduction='none')
        arg_entr.detach_()
        all_argmaxXentropy = torch.cat((all_argmaxXentropy, arg_entr.cpu()))

    # 将全量损失转换为 numpy 数组
    loss_tr = all_losses.data.numpy()

    # -------------------------------
    # 异常值检测（去除极端高低损失）
    # -------------------------------
    max_perc = np.percentile(loss_tr, 95)  # 上 95% 分位数
    min_perc = np.percentile(loss_tr, 5)   # 下 5% 分位数
    loss_tr = loss_tr[(loss_tr <= max_perc) & (loss_tr >= min_perc)]  # 去掉极端值

    # 将最大最小值保存为 Tensor，用于后续归一化
    bmm_model_maxLoss = torch.FloatTensor([max_perc]).to(device)
    bmm_model_minLoss = torch.FloatTensor([min_perc]).to(device) + 1e-5  # 避免除零

    # -------------------------------
    # 损失归一化到 (0,1) 区间
    # -------------------------------
    loss_tr = (loss_tr - bmm_model_minLoss.data.cpu().numpy()) / \
              (bmm_model_maxLoss.data.cpu().numpy() - bmm_model_minLoss.data.cpu().numpy() + 1e-6)

    # 防止越界
    loss_tr[loss_tr >= 1] = 1 - 1e-4
    loss_tr[loss_tr <= 0] = 1e-4

    # -------------------------------
    # 拟合 Beta 混合模型 (BMM)
    # -------------------------------
    bmm_model = BetaMixture1D(max_iters=10)
    bmm_model.fit(loss_tr)        # 使用归一化后的损失拟合
    bmm_model.create_lookup(1)    # 创建查找表，用于快速估计样本属于噪声的后验概率 --- 对同一个样本来说，其属于干净样本分布的概率和属于噪声样本分布的概率之和为1

    # 返回全量损失、概率、基于预测类别的损失，以及拟合的 BMM 和最大最小损失
    return all_losses.data.numpy(), \
           all_probs.data.numpy(), \
           all_argmaxXentropy.numpy(), \
           bmm_model, bmm_model_maxLoss, bmm_model_minLoss

def probability(self, x):
    '''
    计算给定样本 x 的混合概率密度
    
    输入:
    - x: 样本，可以是单个值或数组
    
    输出:
    - 样本在混合 Beta 分布下的总概率密度
    '''
    # 对每个 Beta 分布分量，计算加权似然，然后求和
    return sum(self.weighted_likelihood(x, y) for y in range(2))


def posterior(self, x, y):
    '''
    计算样本 x 属于第 y 个 Beta 分布分量的后验概率 P(y|x)
    
    输入:
    - x: 样本
    - y: 分量索引（0 或 1）
    
    输出:
    - 后验概率 P(y|x)
    '''
    # 后验概率 = 加权似然 / 总概率
    return self.weighted_likelihood(x, y) / (self.probability(x) + self.eps_nan)


def create_lookup(self, y):
    '''
    为指定分量 y 创建后验概率查找表，用于快速估算样本属于该分量的概率
    
    输入:
    - y: 分量索引（0 或 1）
    '''
    # 在 [0,1] 范围内生成均匀的点 -- 损失会被归一化到[0,1]区间中去,lookup_resolution默认为100
    x_l = np.linspace(0+self.eps_nan, 1-self.eps_nan, self.lookup_resolution)
    
    # 计算每个点属于 y 分量的后验概率
    lookup_t = self.posterior(x_l, y)
    
    # 将最大概率点之后的值全部置为最大值，保证查找表单调
    lookup_t[np.argmax(lookup_t):] = lookup_t.max()
    
    # 保存查找表
    self.lookup = lookup_t
    # 保存对应的 x 值（虽然最终没使用）
    self.lookup_loss = x_l


def look_lookup(self, x, loss_max, loss_min):
    '''
    使用查找表快速估算样本的后验概率
    
    输入:
    - x: 样本张量
    - loss_max: 最大损失（用于归一化）
    - loss_min: 最小损失（用于归一化）
    
    输出:
    - 样本对应的查找表后验概率
    '''
    # 转为 numpy 数组
    x_i = x.clone().cpu().numpy()
    
    # 映射到查找表索引
    x_i = np.array((self.lookup_resolution * x_i).astype(int))
    
    # 边界处理
    x_i[x_i < 0] = 0
    x_i[x_i == self.lookup_resolution] = self.lookup_resolution - 1
    
    # 返回查找表对应的概率
    return self.lookup[x_i]

静态 MixUp 数据增强

对输入数据进行 MixUp 增强

def mixup_data(x, y, alpha=1.0, device='cuda'):
    '''
    对输入的 batch 数据进行 Mixup 数据增强

    输入:
    - x: 输入特征张量，形状 [batch_size, ...]
    - y: 对应标签张量，形状 [batch_size, num_classes] 或 [batch_size]
    - alpha: Beta 分布参数，用于生成混合系数 lambda
    - device: 数据所在设备，'cuda' 或 'cpu'

    输出:
    - mixed_x: 混合后的输入特征张量
    - y_a: 原始标签
    - y_b: 对应被混合的另一组标签
    - lam: 混合系数 lambda
    '''
    
    # 1. 根据 alpha 参数生成混合系数 lam
    if alpha > 0:
        lam = np.random.beta(alpha, alpha)  # 从 Beta(alpha, alpha) 分布采样
    else:
        lam = 1  # alpha=0 时，不做混合，相当于直接返回原样本

    # 2. 获取 batch 大小
    batch_size = x.size()[0]

    # 3. 随机打乱 batch 索引，用于选择混合的另一组样本
    if device == 'cuda':
        index = torch.randperm(batch_size).cuda()
    else:
        index = torch.randperm(batch_size)

    # 4. 根据 lambda 对输入特征进行线性混合
    mixed_x = lam * x + (1 - lam) * x[index, :]

    # 5. 对应的标签也要保留两组，用于计算 Mixup 损失
    y_a, y_b = y, y[index]

    # 6. 返回混合后的输入、两组标签以及混合系数
    return mixed_x, y_a, y_b, lam

对输出 Loss 进行MixUp 增强

def mixup_criterion(pred, y_a, y_b, lam):
    return lam * F.nll_loss(pred, y_a) + (1 - lam) * F.nll_loss(pred, y_b)

动态硬自举 + 静态MixUp增强

def mixup_data_Boot(x, y, alpha=1.0, device='cuda'):
    '''Returns mixed inputs, pairs of targets, and lambda'''
    if alpha > 0:
        lam = np.random.beta(alpha, alpha)
    else:
        lam = 1

    batch_size = x.size()[0]
    if device=='cuda':
        index = torch.randperm(batch_size).to(device)
    else:
        index = torch.randperm(batch_size)

    mixed_x = lam * x + (1 - lam) * x[index, :]
    y_a, y_b = y, y[index]
    # 此代码上面已经给出过注释，不过用于自举的时候需要多返回index
    return mixed_x, y_a, y_b, lam, index

def train_mixUp_HardBootBeta(args, model, device, train_loader, optimizer, epoch, alpha, bmm_model, 
                             bmm_model_maxLoss, bmm_model_minLoss, reg_term, num_classes):
    """
    基于 Mixup + Hard Bootstrapping + Beta 混合模型动态权重的训练函数

    参数:
    - args: 配置参数，包括 batch_size、log_interval 等
    - model: 待训练的神经网络模型
    - device: 训练设备 (cuda / cpu)
    - train_loader: 训练数据加载器
    - optimizer: 优化器
    - epoch: 当前训练轮次
    - alpha: Mixup Beta 分布参数
    - bmm_model: Beta 混合模型对象，用于计算噪声权重
    - bmm_model_maxLoss: 训练集最大损失，用于归一化
    - bmm_model_minLoss: 训练集最小损失，用于归一化
    - reg_term: 正则化系数
    - num_classes: 类别数量
    """

    model.train()  # 设置模型为训练模式
    loss_per_batch = []  # 用于保存每个 batch 的损失
    acc_train_per_batch = []  # 用于保存每个 batch 的训练精度
    correct = 0  # 用于累计正确预测样本数

    # 遍历训练集每个 batch
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()  # 清空梯度

        # 1. 对当前 batch 做一次前向传播，获取原始输出
        output_x1 = model(data)
        output_x1.detach_()  # 不计算梯度
        optimizer.zero_grad()

        # 2. Mixup 数据增强，返回混合输入、两组标签、Mixup 系数 lam、索引
        inputs_mixed, targets_1, targets_2, lam, index = mixup_data_Boot(data, target, alpha, device)

        # 对混合样本进行前向传播
        output = model(inputs_mixed)
        output_mean = F.softmax(output, dim=1)  # 转为概率
        tab_mean_class = torch.mean(output_mean, -2)  # 计算每个类别在 batch 中的平均概率
        output = F.log_softmax(output, dim=1)  # 转为 log 概率，用于 NLL loss

        # 3. 使用 Beta 混合模型计算每个样本属于噪声分布的概率 B
        B = compute_probabilities_batch(data, target, model, bmm_model, bmm_model_maxLoss, bmm_model_minLoss)
        B = B.to(device)
        B[B <= 1e-4] = 1e-4  # 避免 B 太小
        B[B >= 1 - 1e-4] = 1 - 1e-4  # 避免 B 太大

        # 4. 准备 Hard Bootstrapping 相关变量
        output_x1 = F.log_softmax(output_x1, dim=1)
        output_x2 = output_x1[index, :]  # 对应 Mixup 中第二组样本
        B2 = B[index]  # 第二组样本的权重

        z1 = torch.max(output_x1, dim=1)[1]  # 第一组样本预测类别索引
        z2 = torch.max(output_x2, dim=1)[1]  # 第二组样本预测类别索引

        # 5. 计算每个样本的 Hard Bootstrapping 损失
        # 第一组真实标签损失
        loss_x1_vec = (1 - B) * F.nll_loss(output, targets_1, reduction='none')
        loss_x1 = torch.sum(loss_x1_vec) / len(loss_x1_vec)

        # 第一组预测类别损失（噪声主导）
        loss_x1_pred_vec = B * F.nll_loss(output, z1, reduction='none')
        loss_x1_pred = torch.sum(loss_x1_pred_vec) / len(loss_x1_pred_vec)

        # 第二组真实标签损失
        loss_x2_vec = (1 - B2) * F.nll_loss(output, targets_2, reduction='none')
        loss_x2 = torch.sum(loss_x2_vec) / len(loss_x2_vec)

        # 第二组预测类别损失（噪声主导）
        loss_x2_pred_vec = B2 * F.nll_loss(output, z2, reduction='none')
        loss_x2_pred = torch.sum(loss_x2_pred_vec) / len(loss_x2_pred_vec)

        # 6. 根据 Mixup 系数 lam 加权组合两组损失
        loss = lam*(loss_x1 + loss_x1_pred) + (1-lam)*(loss_x2 + loss_x2_pred)

        # 7. 类别概率均匀性正则化
        loss_reg = reg_loss_class(tab_mean_class, num_classes)
        loss = loss + reg_term * loss_reg

        # 8. 反向传播与参数更新
        loss.backward()
        optimizer.step()

        # 9. 监控每个 batch 的损失
        loss_per_batch.append(loss.item())

        # 10. 保存训练精度
        pred = output.max(1, keepdim=True)[1]  # 预测类别索引
        correct += pred.eq(target.view_as(pred)).sum().item()
        acc_train_per_batch.append(100. * correct / ((batch_idx+1)*args.batch_size))

        # 11. 打印训练日志
        if batch_idx % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}, Accuracy: {:.0f}%, Learning rate: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item(),
                100. * correct / ((batch_idx + 1) * args.batch_size),
                optimizer.param_groups[0]['lr']))

    # 12. 计算 epoch 平均损失和精度
    loss_per_epoch = [np.average(loss_per_batch)]
    acc_train_per_epoch = [np.average(acc_train_per_batch)]

    return (loss_per_epoch, acc_train_per_epoch)

def compute_probabilities_batch(data, target, cnn_model, bmm_model, bmm_model_maxLoss, bmm_model_minLoss):
    cnn_model.eval()
    outputs = cnn_model(data)
    outputs = F.log_softmax(outputs, dim=1)
    batch_losses = F.nll_loss(outputs.float(), target, reduction = 'none')
    batch_losses.detach_()
    outputs.detach_()
    cnn_model.train()
    # 损失归一化，异常值边界化
    batch_losses = (batch_losses - bmm_model_minLoss) / (bmm_model_maxLoss - bmm_model_minLoss + 1e-6)
    batch_losses[batch_losses >= 1] = 1-10e-4
    batch_losses[batch_losses <= 0] = 10e-4

    #B = bmm_model.posterior(batch_losses,1)
    # 查表快速得到每个样本损失属于beta2分布的概率(估算)
    B = bmm_model.look_lookup(batch_losses, bmm_model_maxLoss, bmm_model_minLoss)

    return torch.FloatTensor(B)

# KL 散度
def reg_loss_class(mean_tab,num_classes=10):
    loss = 0
    for items in mean_tab:
        loss += (1./num_classes)*torch.log((1./num_classes)/items)
    return loss

动态软自举 + 静态MixUp增强

def train_mixUp_SoftBootBeta(args, model, device, train_loader, optimizer, epoch, alpha, bmm_model, bmm_model_maxLoss, \
                                            bmm_model_minLoss, reg_term, num_classes):
    """
    训练函数：MixUp + Soft Bootstrapping + Beta Mixture Model
    - 使用 MixUp 数据增强
    - 使用 Soft Bootstrapping（结合模型预测分布与真实标签）
    - 使用 BMM 模型估计样本是否为干净样本的概率 B
    - 使用类别分布正则化防止过拟合
    """

    model.train()  # 设置为训练模式
    loss_per_batch = []  # 记录每个 batch 的 loss
    acc_train_per_batch = []  # 记录每个 batch 的训练集精度
    correct = 0  # 累积正确预测的数量

    # 遍历所有 batch
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()  # 梯度清零

        # 第一次前向传播：得到原始样本的预测结果
        output_x1 = model(data)
        output_x1.detach_()  # 切断梯度，不参与反向传播
        optimizer.zero_grad()

        # 估计每个样本的干净概率 B
        if epoch == 1:
            # 第一个 epoch 没法建模，统一设置为 0.5
            B = 0.5*torch.ones(len(target)).float().to(device)
        else:
            # 通过 Beta Mixture Model 估计每个样本的干净概率
            B = compute_probabilities_batch(data, target, model, bmm_model, bmm_model_maxLoss, bmm_model_minLoss)
            B = B.to(device)
            # 防止数值极端情况，限制在 [1e-4, 1-1e-4] 区间内
            B[B <= 1e-4] = 1e-4
            B[B >= 1-1e-4] = 1-1e-4

        # MixUp 数据增强：混合两个样本（输入和标签）
        inputs_mixed, targets_1, targets_2, lam, index = mixup_data_Boot(data, target, alpha, device)

        # 前向传播：得到混合样本的预测结果
        output = model(inputs_mixed)
        output_mean = F.softmax(output, dim=1)  # softmax 概率分布
        output = F.log_softmax(output, dim=1)   # log-softmax 结果（供 NLLLoss 使用）

        # 提取被 mixup 的第二个样本对应的预测结果
        output_x2 = output_x1[index, :]

        # 统计所有类别的平均预测概率，用于正则化
        tab_mean_class = torch.mean(output_mean, -2)  # 按样本维度取均值

        # 计算 Soft Bootstrapping 的混合损失
        # - targets_1, targets_2: mixup 后的原始标签
        # - output_x1, output_x2: 模型 soft label 预测结果
        # - B: 每个样本为干净的概率
        # - lam: mixup 权重
        loss = mixup_criterion_mixSoft(output, targets_1, targets_2, B, lam, index, output_x1, output_x2)

        # 加上类别分布正则项，避免预测过度偏向某些类别
        loss_reg = reg_loss_class(tab_mean_class)
        loss = loss + reg_term*loss_reg

        # 反向传播 + 参数更新
        loss.backward()
        optimizer.step()

        ################## monitor losses  ####################################
        loss_per_batch.append(loss.item())  # 保存 batch 的损失
        ########################################################################

        # 计算 batch 的训练精度
        pred = output.max(1, keepdim=True)[1]  # 预测类别 = 最大 log 概率对应的类别
        correct += pred.eq(target.view_as(pred)).sum().item()  # 累积正确数量
        acc_train_per_batch.append(100. * correct / ((batch_idx+1)*args.batch_size))

        # 定期打印日志
        if batch_idx % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}, Accuracy: {:.0f}%, Learning rate: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item(),
                       100. * correct / ((batch_idx + 1) * args.batch_size),
                optimizer.param_groups[0]['lr']))

    # 统计一个 epoch 的平均 loss 和 acc
    loss_per_epoch = [np.average(loss_per_batch)]
    acc_train_per_epoch = [np.average(acc_train_per_batch)]

    return (loss_per_epoch, acc_train_per_epoch)

def mixup_criterion_mixSoft(pred, y_a, y_b, B, lam, index, output_x1, output_x2):
    """
    计算 MixUp + Soft Bootstrapping 的损失函数
    Args:
        pred      : log-softmax 输出 (batch_size, num_classes)
        y_a, y_b  : mixup 的两个标签
        B         : 每个样本为“干净样本”的概率 (batch_size,)
        lam       : mixup 系数 (Beta 分布采样得到的混合比例)
        index     : 打乱顺序的索引，用于取出第二组样本
        output_x1 : 原始 batch 的模型输出 (未打乱)
        output_x2 : 打乱后的模型输出 (对应 y_b 的样本)
    Returns:
        标量 loss （一个 batch 的平均损失）
    """

    return torch.sum(
        # ----------- 第一部分：lam 权重对应的混合样本 -----------
        (lam) * (
            # (1 - B)：更多信任真实标签 → 使用 NLLLoss
            (1 - B) * F.nll_loss(pred, y_a, reduction='none') +

            # B：更多信任模型预测（Soft Bootstrapping）
            #   -torch.sum(p_soft * log_pred)，即交叉熵形式
            B * (-torch.sum(F.softmax(output_x1, dim=1) * pred, dim=1))
        )
        +
        # ----------- 第二部分：(1-lam) 权重对应的另一半混合样本 -----------
        (1 - lam) * (
            # (1 - B[index])：信任真实标签 y_b
            (1 - B[index]) * F.nll_loss(pred, y_b, reduction='none') +

            # B[index]：信任打乱后的样本 soft label
            B[index] * (-torch.sum(F.softmax(output_x2, dim=1) * pred, dim=1))
        )
    ) / len(pred)  # 对 batch 求平均

soft label 是直接每个类别乘上其对应的软概率值，再把所有类别的概率值求和，得到当前样本的软损失。

动态MixUp增强

def train_mixUp_Beta(args, model, device, train_loader, optimizer, epoch, alpha, bmm_model,
                                bmm_model_maxLoss, bmm_model_minLoss):
    # 设置模型为训练模式
    model.train()
    loss_per_batch = []  # 用于记录每个 batch 的 loss

    acc_train_per_batch = []  # 用于记录每个 batch 的训练精度
    correct = 0  # 统计累计预测正确的样本数

    # 遍历每个 batch
    for batch_idx, (data, target) in enumerate(train_loader):

        # 将数据和标签放到 GPU/CPU
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()  # 梯度清零

        # 第一个 epoch 用固定 B=0.5，表示一开始不区分干净样本和噪声样本
        if epoch == 1:
            B = 0.5 * torch.ones(len(target)).float().to(device)
        else:
            # 从 Beta 混合模型中计算每个样本属于“干净样本”的概率 B
            B = compute_probabilities_batch(data, target, model, bmm_model, bmm_model_maxLoss, bmm_model_minLoss)
            B = B.to(device)
            # 限制 B 的取值范围，避免数值不稳定（太接近 0 或 1）
            B[B <= 1e-4] = 1e-4
            B[B >= 1 - 1e-4] = 1 - 1e-4

        # 使用 B 控制 mixup 的动态权重，生成混合样本和混合标签
        inputs_mixed, targets_1, targets_2, index = mixup_data_beta(data, target, B, device)

        # 前向传播
        output = model(inputs_mixed)
        output = F.log_softmax(output, dim=1)  # 输出转 log-softmax，用于 NLLLoss

        # 计算 MixUp 的损失（Beta 动态控制的 mixup loss）
        loss = mixup_criterion_beta(output, targets_1, targets_2)

        # 反向传播
        loss.backward()

        # 更新参数
        optimizer.step()

        ################## monitor losses  ####################################
        loss_per_batch.append(loss.item())  # 保存该 batch 的 loss
        ########################################################################

        # 保存训练精度：取 log-probability 最大的类别作为预测
        pred = output.max(1, keepdim=True)[1]  # 预测类别
        correct += pred.eq(target.view_as(pred)).sum().item()  # 累积正确个数
        acc_train_per_batch.append(100. * correct / ((batch_idx + 1) * args.batch_size))  # 当前平均精度

        # 打印训练状态（每 log_interval 个 batch 打印一次）
        if batch_idx % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}, Accuracy: {:.0f}%, Learning rate: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item(),
                       100. * correct / ((batch_idx + 1) * args.batch_size),
                optimizer.param_groups[0]['lr']))

    # 计算每个 epoch 的平均 loss 和 accuracy
    loss_per_epoch = [np.average(loss_per_batch)]
    acc_train_per_epoch = [np.average(acc_train_per_batch)]

    return (loss_per_epoch, acc_train_per_epoch)

def mixup_data_beta(x, y, B, device='cuda'):
    '''
    基于 Beta 混合模型 (BMM) 概率 B 来生成 MixUp 的样本。
    输入：
        x: 输入图像 batch，形状 [batch_size, C, H, W]
        y: 输入标签 batch，形状 [batch_size]
        B: 每个样本的 Beta 概率（表示该样本干净的概率），形状 [batch_size]
        device: 使用的设备（默认 'cuda'）
    输出：
        mixed_x: MixUp 后的输入图像
        y_a, y_b: MixUp 对应的两个标签
        index: 被打乱的索引（用于混合的另一半样本）
    '''

    batch_size = x.size()[0]  # 当前 batch 的大小
    
    # 随机打乱索引，用于 MixUp 配对
    if device == 'cuda':
        index = torch.randperm(batch_size).cuda()
    else:
        index = torch.randperm(batch_size)

    # 计算归一化因子 lam
    # lam = (1 - B_i) + (1 - B_j)，保证加权后的比例能正确归一化
    lam = ((1 - B) + (1 - B[index]))

    # 动态 MixUp：
    #   1-B : 表示样本是 "干净" 的概率
    #   按照样本的干净概率加权混合两个图像，干净样本贡献大，噪声样本贡献小
    #   权重 = (1-B) / lam   和   (1-B[index]) / lam
    mixed_x = ((1 - B) / lam).unsqueeze(1).unsqueeze(2).unsqueeze(3) * x + \
              ((1 - B[index]) / lam).unsqueeze(1).unsqueeze(2).unsqueeze(3) * x[index, :]

    # 返回标签对：y 和打乱后的 y[index]
    y_a, y_b = y, y[index]

    return mixed_x, y_a, y_b, index


def mixup_criterion_beta(pred, y_a, y_b):
    lam = np.random.beta(32, 32)
    return lam * F.nll_loss(pred, y_a) + (1-lam) * F.nll_loss(pred, y_b)

动态MixUp增强 + 动态自举 + 温度调节

def train_mixUp_SoftHardBetaDouble(args, model, device, train_loader, optimizer, epoch, bmm_model, \
                                    bmm_model_maxLoss, bmm_model_minLoss, countTemp, k, temp_length, reg_term, num_classes):
    """
    训练函数：Dynamic MixUp + Soft/Hard Bootstrapping + Beta混合权重 + 温度调节
    """
    model.train()  # 设置模型为训练模式
    loss_per_batch = []  # 用于记录每个batch的损失
    acc_train_per_batch = []  # 用于记录每个batch的训练精度
    correct = 0  # 累计正确预测数

    steps_every_n = 2  # 每经过2个epoch调整一次温度索引k
    temp_vec = np.linspace(1, 0.001, temp_length)  # 温度衰减序列

    # 遍历训练数据集
    for batch_idx, (data, target) in enumerate(train_loader):

        # 将数据和标签放到指定设备上
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()  # 梯度清零

        # 对当前batch进行一次前向传播，得到原始预测
        output_x1 = model(data)
        output_x1.detach_()  # 阻止梯度回传到这里
        optimizer.zero_grad()

        # 计算样本属于噪声分布的概率B
        if epoch == 1:
            # 第1个epoch默认均匀概率0.5
            B = 0.5 * torch.ones(len(target)).float().to(device)
        else:
            # 后续epoch使用Beta混合模型预测
            B = compute_probabilities_batch(data, target, model, bmm_model, bmm_model_maxLoss, bmm_model_minLoss)
            B = B.to(device)
            # 防止概率为0或1导致数值问题
            B[B <= 1e-4] = 1e-4
            B[B >= 1-1e-4] = 1-1e-4

        # 使用Beta权重进行动态MixUp
        inputs_mixed, targets_1, targets_2, index = mixup_data_beta(data, target, B, device)
        output = model(inputs_mixed)  # 对混合后的样本前向传播
        output_mean = F.softmax(output, dim=1)  # 得到混合样本的softmax概率
        output = F.log_softmax(output, dim=1)  # log_softmax用于计算NLLLoss
        output_x2 = output_x1[index, :]  # 根据混合索引获取对应的原始预测
        tab_mean_class = torch.mean(output_mean,-2)  # 计算每个类别的平均概率，用于正则化

        # 选择当前温度
        Temp = temp_vec[k]

        # 计算Soft/Hard MixUp损失
        loss = mixup_criterion_SoftHard(output, targets_1, targets_2, B, index, output_x1, output_x2, Temp)

        # 类别分布正则化
        loss_reg = reg_loss_class(tab_mean_class, num_classes)
        loss = loss + reg_term*loss_reg

        # 反向传播
        loss.backward()
        optimizer.step()

        ################## 监控loss ####################################
        loss_per_batch.append(loss.item())
        #################################################################

        # 保存训练精度
        pred = output.max(1, keepdim=True)[1]  # 取每个样本预测最大概率的类别索引
        correct += pred.eq(target.view_as(pred)).sum().item()  # 累计正确预测数
        acc_train_per_batch.append(100. * correct / ((batch_idx+1)*args.batch_size))  # 当前batch平均精度

        # 日志打印
        if batch_idx % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}, Accuracy: {:.0f}%, Learning rate: {:.6f}, Temperature: {:.4f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item(),
                       100. * correct / ((batch_idx + 1) * args.batch_size),
                optimizer.param_groups[0]['lr'], Temp))

    # 计算当前epoch平均损失和精度
    loss_per_epoch = [np.average(loss_per_batch)]
    acc_train_per_epoch = [np.average(acc_train_per_batch)]

    # 更新温度索引，每steps_every_n个epoch更新一次
    countTemp = countTemp + 1
    if countTemp == steps_every_n:
        k = k + 1
        k = min(k, len(temp_vec) - 1)  # 防止索引越界
        countTemp = 1

    return (loss_per_epoch, acc_train_per_epoch, countTemp, k)

def mixup_criterion_SoftHard(pred, y_a, y_b, B, index, output_x1, output_x2, Temp):
    """
    计算Soft/Hard Bootstrapping + MixUp损失
    说明：
    - pred: 模型对混合样本的log_softmax输出
    - y_a, y_b: 原始样本标签，对应混合前的两个样本
    - B: 样本属于噪声分布的概率 (Beta权重)
    - index: 混合索引，对应第二个样本
    - output_x1, output_x2: 原始样本前向传播得到的log_softmax输出
    - Temp: 温度参数，用于控制soft label的平滑程度
    """
    
    # 对每个样本计算Soft/Hard损失
    # 对第一个样本：
    # (1 - B) * F.nll_loss(pred, y_a) -> 保留ground-truth标签的损失 (Hard部分)
    # B * (-torch.sum(F.softmax(output_x1/Temp) * pred)) -> 利用模型预测的soft标签进行损失计算 (Soft部分)
    # 对第二个样本同理，使用B[index]和output_x2
    loss = torch.sum(
        (0.5) * (
                (1 - B) * F.nll_loss(pred, y_a, reduction='none') + 
                B * (-torch.sum(F.softmax(output_x1/Temp, dim=1) * pred, dim=1))
        ) +
        (0.5) * (
                (1 - B[index]) * F.nll_loss(pred, y_b, reduction='none') + 
                B[index] * (-torch.sum(F.softmax(output_x2/Temp, dim=1) * pred, dim=1))
        )
    ) / len(pred)  # 对batch中的所有样本取平均

    return loss

Hard部分： (1 - B) * F.nll_loss(pred, y_a)
- 对干净样本，保留ground-truth标签损失。
Soft部分： B * (-torch.sum(F.softmax(output_x1/Temp) * pred))
- 对噪声样本，用模型预测的概率（经过温度平滑）作为soft label计算损失。
MixUp融合：
- 使用 0.5 权重对两个混合样本的损失取平均。
温度Temp：
- 控制soft label的平滑程度，值越小越接近one-hot，值越大越平滑。
返回值：
- 对整个batch的样本损失取平均。

训练核心主流程

def main():
    # 初始化BMM模型及相关参数
    bmm_model = bmm_model_maxLoss = bmm_model_minLoss = cont = k = 0

    # bootstrap阶段标准训练结束的epoch，+1是因为条件定义为 ">" 或 "<" 而不是 ">="
    bootstrap_ep_std = milestones[0] + 5 + 1
    # 引导式Mixup开始的epoch
    guidedMixup_ep = 106

    # 动态Mixup情况下，bootstrap阶段的epoch
    if args.Mixup == 'Dynamic':
        bootstrap_ep_mixup = guidedMixup_ep + 5
    else:
        bootstrap_ep_mixup = milestones[0] + 5 + 1

    # 用于Soft-Hard Beta的温度控制
    countTemp = 1
    temp_length = 200 - bootstrap_ep_mixup

    # 遍历每个训练epoch
    for epoch in range(1, args.epochs + 1):
        # 更新学习率调度器
        scheduler.step()

        ### 标准交叉熵训练（不使用Mixup） ###
        if args.Mixup == "None":
            print('\t##### Doing standard training with cross-entropy loss #####')
            loss_per_epoch, acc_train_per_epoch_i = train_CrossEntropy(args, model, device, train_loader, optimizer, epoch)

        ### 静态Mixup ###
        if args.Mixup == "Static":
            alpha = args.alpha
            bootstrap_ep_mixup = 0
            # 前几个epoch进行普通Mixup训练
            if epoch < bootstrap_ep_mixup:
                print('\t##### Doing NORMAL mixup for {0} epochs #####'.format(bootstrap_ep_mixup - 1))
                loss_per_epoch, acc_train_per_epoch_i = train_mixUp(args, model, device, train_loader, optimizer, epoch, 32)
            else:
                # 后续epoch进行Beta Bootstrapping（Hard或Soft）与普通Mixup结合训练
                if args.BootBeta == "Hard":
                    print("\t##### Doing HARD BETA bootstrapping and NORMAL mixup from the epoch {0} #####".format(bootstrap_ep_mixup))
                    loss_per_epoch, acc_train_per_epoch_i = train_mixUp_HardBootBeta(
                        args, model, device, train_loader, optimizer, epoch,
                        alpha, bmm_model, bmm_model_maxLoss, bmm_model_minLoss,
                        args.reg_term, num_classes
                    )
                elif args.BootBeta == "Soft":
                    print("\t##### Doing SOFT BETA bootstrapping and NORMAL mixup from the epoch {0} #####".format(bootstrap_ep_mixup))
                    loss_per_epoch, acc_train_per_epoch_i = train_mixUp_SoftBootBeta(
                        args, model, device, train_loader, optimizer, epoch,
                        alpha, bmm_model, bmm_model_maxLoss, bmm_model_minLoss,
                        args.reg_term, num_classes
                    )

        ## 动态Mixup ##
        if args.Mixup == "Dynamic":
            alpha = args.alpha
            # 前几个epoch进行普通Mixup训练
            if epoch < guidedMixup_ep:
                print('\t##### Doing NORMAL mixup for {0} epochs #####'.format(guidedMixup_ep - 1))
                loss_per_epoch, acc_train_per_epoch_i = train_mixUp(args, model, device, train_loader, optimizer, epoch, 32)
            # guidedMixup阶段使用Beta混合分布进行Mixup
            elif epoch < bootstrap_ep_mixup:
                print('\t##### Doing Dynamic mixup from epoch {0} #####'.format(guidedMixup_ep))
                loss_per_epoch, acc_train_per_epoch_i = train_mixUp_Beta(
                    args, model, device, train_loader, optimizer, epoch, alpha,
                    bmm_model, bmm_model_maxLoss, bmm_model_minLoss
                )
            # Soft-Hard Beta与动态Mixup结合训练，并使用温度控制
            else:
                print("\t##### Going from SOFT BETA bootstrapping to HARD BETA with linear temperature and Dynamic mixup from the epoch {0} #####".format(bootstrap_ep_mixup))
                loss_per_epoch, acc_train_per_epoch_i, countTemp, k = train_mixUp_SoftHardBetaDouble(
                    args, model, device, train_loader, optimizer, epoch,
                    bmm_model, bmm_model_maxLoss, bmm_model_minLoss,
                    countTemp, k, temp_length, args.reg_term, num_classes
                )

        ### 跟踪训练损失和BMM模型 ###
        epoch_losses_train, epoch_probs_train, argmaxXentropy_train, bmm_model, bmm_model_maxLoss, bmm_model_minLoss = \
            track_training_loss(args, model, device, train_loader_track, epoch, bmm_model, bmm_model_maxLoss, bmm_model_minLoss)

        # 测试阶段
        loss_per_epoch, acc_val_per_epoch_i = test_cleaning(args, model, device, test_loader)

训练数据上添加噪声

# Noise without the sample class
def add_noise_cifar_wo(loader, noise_percentage=20):
    """
    给 CIFAR 训练集添加噪声标签，但新标签不能与原标签相同。
    
    参数:
        loader: CIFAR 数据加载器
        noise_percentage: 需要添加噪声的百分比（0~100）
    
    返回:
        noisy_labels: 添加噪声后的标签列表
    """
    # 固定随机种子，保证实验可复现
    torch.manual_seed(2)
    np.random.seed(42)
    
    # 复制训练标签
    noisy_labels = [sample_i for sample_i in loader.sampler.data_source.train_labels]
    # 复制训练图像
    images = [sample_i for sample_i in loader.sampler.data_source.train_data]
    
    # 生成每个样本是否加噪声的随机数（0~99）
    probs_to_change = torch.randint(100, (len(noisy_labels),))
    # 判断哪些样本需要加噪声
    idx_to_change = probs_to_change >= (100.0 - noise_percentage)
    # 计算实际噪声比例（仅用于信息输出）
    percentage_of_bad_labels = 100 * (torch.sum(idx_to_change).item() / float(len(noisy_labels)))

    # 对每个需要加噪声的样本进行处理
    for n, label_i in enumerate(noisy_labels):
        if idx_to_change[n] == 1:
            # 构建新标签候选集合，不包含当前原标签
            set_labels = list(set(range(10)) - set([label_i]))
            # 随机选择一个新标签
            set_index = np.random.randint(len(set_labels))
            noisy_labels[n] = set_labels[set_index]

    # 更新 DataLoader 中的数据和标签
    loader.sampler.data_source.train_data = images
    loader.sampler.data_source.train_labels = noisy_labels

    return noisy_labels


# Noise with the sample class (as in Re-thinking generalization)
def add_noise_cifar_w(loader, noise_percentage=20):
    """
    给 CIFAR 训练集添加噪声标签，但新标签可以包含原标签（参考论文 "Re-thinking generalization"）。
    
    参数:
        loader: CIFAR 数据加载器
        noise_percentage: 需要添加噪声的百分比（0~100）
    
    返回:
        noisy_labels: 添加噪声后的标签列表
    """
    # 固定随机种子，保证实验可复现
    torch.manual_seed(2)
    np.random.seed(42)
    
    # 复制训练标签
    noisy_labels = [sample_i for sample_i in loader.sampler.data_source.train_labels]
    # 复制训练图像
    images = [sample_i for sample_i in loader.sampler.data_source.train_data]
    
    # 生成每个样本是否加噪声的随机数（0~99）
    probs_to_change = torch.randint(100, (len(noisy_labels),))
    # 判断哪些样本需要加噪声
    idx_to_change = probs_to_change >= (100.0 - noise_percentage)
    # 计算实际噪声比例（仅用于信息输出）
    percentage_of_bad_labels = 100 * (torch.sum(idx_to_change).item() / float(len(noisy_labels)))

    # 对每个需要加噪声的样本进行处理
    for n, label_i in enumerate(noisy_labels):
        if idx_to_change[n] == 1:
            # 构建新标签候选集合，包含所有可能标签（包括原标签）
            set_labels = list(set(range(10)))
            # 随机选择一个新标签
            set_index = np.random.randint(len(set_labels))
            noisy_labels[n] = set_labels[set_index]

    # 更新 DataLoader 中的数据和标签
    loader.sampler.data_source.train_data = images
    loader.sampler.data_source.train_labels = noisy_labels

    return noisy_labels

附录

本节在主论文的基础上，对提出的无监督 Beta 混合模型（BMM）进行扩展讨论，提供更多细节。

低标签噪声下的 BMM 性能

我们希望在标签噪声存在的情况下实现稳健的表示学习，这种噪声可能在自动标注的图像中出现。在几乎无噪声（接近 0%）的精心标注数据集上，性能可能下降，因为损失分布不再是双组分混合。在这种情况下，BMM 几乎会将所有样本分类为干净样本，但仍可能存在一些估计误差，导致有时依赖错误的网络预测而非真实干净标签。然而，对于 20% 的标签噪声，我们在训练结束时仍优于比较的最先进方法，显示出在低噪声水平下的鲁棒性提升。

BMM 参数估计频率

一旦开始进行损失修正（即初始 warm-up 阶段如 4.1 节所述，不进行损失修正），BMM 参数会在每个训练周期后重新估计，通过使用原始（可能含噪声）标签的前向传播计算交叉熵损失。我们还测试了 M-DYR-H（CIFAR-10, 80% 标签噪声）在不同估计周期下的表现：5 个 epoch 和 0.5 个 epoch，发现精度没有下降。原始配置（如图 4(a) 所示）在最佳/最后一次分别达到 86.8 / 86.6，而每 5 个 epoch 重新估计分别为 86.9 / 86.8，每 0.5 个 epoch 为 88.0 / 87.5。

BMM 分类精度与鲁棒性

图 4(b) 展示了 BMM 在训练过程中干净/噪声样本分类能力的 AUC（曲线下面积）演化，显示性能和鲁棒性在不同噪声水平下保持一致。特别是在 CIFAR-10 上，M-DYR-H 在 20%、50% 和 80% 标签噪声下的 AUC 均超过 0.98。训练过程中 AUC 不断增加，对于低噪声水平增加更快，显示出 BMM 随时间对干净/噪声样本判别能力越来越好，并保持一致性预测。

BMM 分类精度对图像分类准确率的影响

BMM 的预测精度对高图像分类准确率至关重要，如图 4(a) 和 4(b) 所示，图像分类准确率与 BMM 分类精度呈同步上升趋势，尤其在高噪声水平下更为明显。图 4(c) 进一步验证了这一关系，通过将 BMM 与 GMM（高斯混合模型）在 CIFAR-10 上进行对比（M-DYR-H，80% 标签噪声）。GMM 的干净/噪声判别能力较差，图像分类准确率也下降（干净/噪声 AUC 从 0.98 降至 0.94，图像分类准确率从 86.6 降至 83.5）。

BMM 对性能的贡献

引入 BMM 得到的损失不仅仅是正则化效果。通过移除 BMM 并在自举损失中使用固定权重（将 0.8 权重分配给 GT，0.2 权重分配给网络预测，同时保持 mixup 增强稳健性），性能会显著下降。在 CIFAR-10 80% 标签噪声下，M-DYR-H 的最后 epoch 准确率从 86.6 降至 74.6。