噪声一致性学习领域相关论文速览

噪声一致性学习领域相关论文速览

A Closer Look at Memorization in Deep Networks

本文前传(扩展阅读): UNDERSTANDING DEEP LEARNING REQUIRES RETHINKING GENERALIZATION

论文核心重点内容:

1. 记忆与泛化的区别

• DNN 可以轻松拟合随机噪声数据，但在真实数据上，模型并不是简单的死记硬背。

• 模型在训练真实数据时优先学习简单模式，只有在复杂模式学习完之后才可能出现记忆行为。

---

2. 训练数据对学习行为的重要性

• DNN 的记忆能力与泛化能力不仅依赖网络结构和优化方法，还与训练数据本身密切相关。

• 训练集中的噪声比例、数据量以及数据本身的复杂度都会显著影响模型的学习动态。

• 实验发现：噪声数据需要更多训练时间和更大容量，而真实数据即使容量较小也能有效学习。

---

3. 正则化对记忆行为的调控

• 显式正则化（如 Dropout、输入噪声、权重衰减、对抗训练）能够抑制模型对随机数据的记忆速度，但对真实数据的泛化影响较小。

• Dropout + 对抗训练最有效：

  • 阻止模型死记硬背噪声

  • 保留对真实数据模式的学习能力

• 说明正则化不仅仅是防止过拟合，也能引导模型优先学习有意义的模式。

---

4. 深度学习优化与模式学习

• 基于 SGD 的优化天然倾向于先学习简单模式，而不是直接记忆每个样本。

• 这种“内容感知”的优化行为解释了 DNN 在过参数化情况下仍能泛化的现象。

• 临界样本比率（CSR）和 loss-sensitivity 指标揭示了模型学习复杂模式和记忆噪声的过程。

---

5. 有效容量（Effective Capacity）与模型行为

• DNN 的有效容量（Effective Capacity）远大于实际训练过程中 SGD 可达到的假设集合，即有效容量。

• 有效容量受模型结构、训练步骤、正则化以及数据特性共同影响。

• 提出了数据依赖的 DNN 容量理解，强调泛化不仅依赖模型本身，也依赖数据集属性。

---

结论与启示:

• 模型在训练真实数据时主要依赖模式学习，而不是死记硬背；噪声数据则必须依赖记忆。

• 深度学习先验（分布式表示、层次化结构）在找到可泛化解中起重要作用。

• 对未来研究的启示：

  • 更加关注数据集属性对 DNN 行为的影响

  • 构建数据依赖的容量理解模型

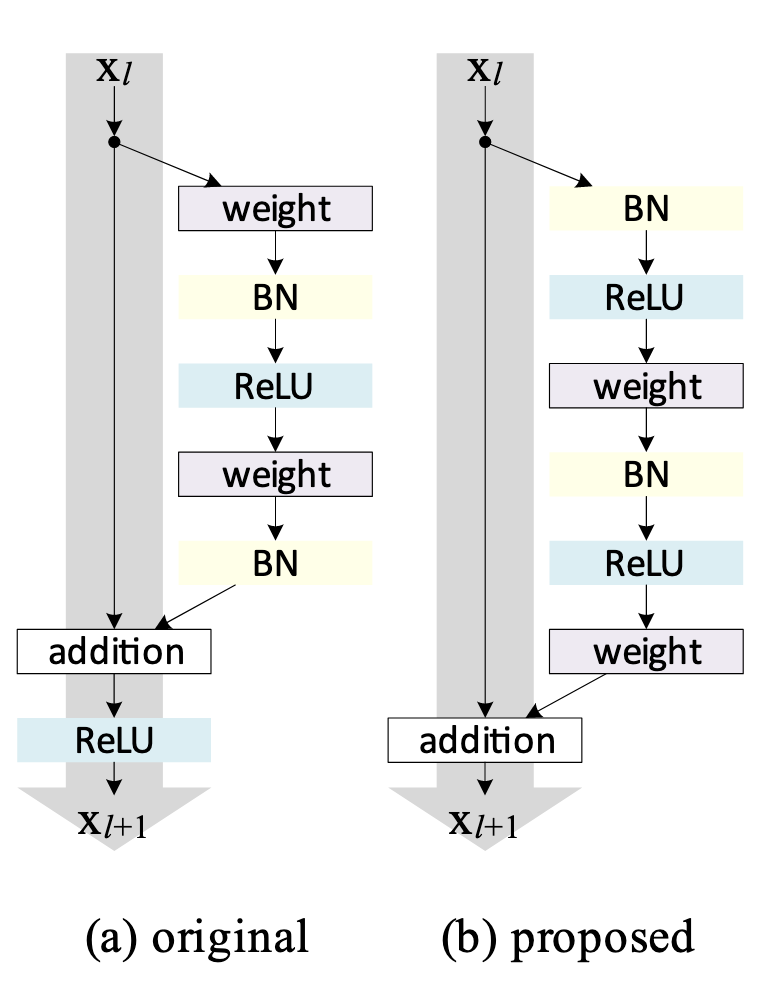
Identity Mappings in Deep Residual Networks

论文观点: 恒等捷径与前激活残差单元是实现超深网络（1000 层以上）可训练且泛化更强的关键设计。

Co-teaching: Robust Training of Deep Neural Networks with Extremely Noisy Labels

Co-teaching 的核心思想是同时训练两个深度网络。在每个小批量训练中，每个网络会根据 小损失（small-loss）标准挑选出一部分样本作为“干净”数据，然后将这些样本交给同伴网络用于更新参数。因此，整个方法被称为 Co-teaching。由于深度学习通常基于 随机梯度下降（SGD），Co-teaching 也以小批量方式运行。

具体过程如下：我们维护两个网络 $f$（参数 $w_f$）和 $g$（参数 $w_g$）。当小批量 $\overline{D}$ 被采样后，$f$（或 $g$）会从中挑选损失最小的部分样本，记为 ${\overline{D}}_f$（或 ${\overline{D}}_g$）。挑选的样本数量由函数 $R(T)$ 控制，即只选择当前小批量中损失最小的 $R(T)$ 百分比样本。然后，将这些挑选出的样本传递给同伴网络，用于更新其参数。

Q1. 为什么基于动态 $R(T)$ 挑选小损失样本能够帮助找到干净样本？

• 直观上，小损失样本更有可能是正确标注的样本。

• 深度网络的 记忆效应 提供了支持：即使数据集中存在噪声标签，深度网络在训练初期会优先学习干净、易识别的模式。因此，在训练早期，小损失标准能够过滤掉大部分噪声样本。

• 但如果训练时间过长，网络会逐渐过拟合噪声标签。为避免这种情况，$R(T)$ 在训练初期应较大，以保留更多样本；随后逐步减小，以提高过滤噪声的效果 。

Q2. 为什么需要两个网络并进行交叉更新？

• 如果只用一个网络，它可能会像 Boosting 或主动学习那样自我演化，但这些方法对噪声和异常值非常敏感，容易因少量错误样本而导致整体性能下降。

• 使用两个网络的优势在于：不同分类器会形成不同决策边界，因此能以不同方式过滤噪声标签。

• 在 Co-teaching 中，网络 $f$ 会用 $g$ 挑选的小损失样本更新参数，反之亦然。这种交叉训练机制类似于“同伴审阅”：学生自己检查作业容易忽略错误，但让同伴检查更容易发现问题。

• 由于一个网络的误差不会直接反馈给自身，交叉更新可以减少自我误差累积的风险，从而在噪声环境下更鲁棒。

Co-teaching 算法实现如下:

# 定义 Co-teaching 损失函数
def loss_coteaching(y_1, y_2, t, forget_rate, ind, noise_or_not):
    """
    y_1, y_2: 两个网络的输出 logits (batch_size x num_classes)
    t: 真实标签 (batch_size)
    forget_rate: 忘记率，表示要丢弃的噪声样本比例
    ind: 当前 batch 样本在整个数据集中的索引，用于追踪噪声标签
    noise_or_not: 布尔数组，表示样本是否为干净样本（True/False）
    """

    # 1. 计算每个网络对每个样本的逐样本交叉熵损失
    loss_1 = F.cross_entropy(y_1, t, reduce=False)  # 不进行平均，保留每个样本的损失
    ind_1_sorted = np.argsort(loss_1.data.cpu().numpy())  # 按损失从小到大排序，得到索引
    loss_1_sorted = loss_1[ind_1_sorted]  # 排序后的 loss

    loss_2 = F.cross_entropy(y_2, t, reduce=False)
    ind_2_sorted = np.argsort(loss_2.data.cpu().numpy())
    loss_2_sorted = loss_2[ind_2_sorted]

    # 2. 计算保留样本的数量
    remember_rate = 1 - forget_rate  # 保留率 = 1 - 忘记率
    num_remember = int(remember_rate * len(loss_1_sorted))  # 保留样本数量

    # 3. 统计保留样本中干净标签的比例（用于评估）
    pure_ratio_1 = np.sum(noise_or_not[ind[ind_1_sorted[:num_remember]]]) / float(num_remember)
    pure_ratio_2 = np.sum(noise_or_not[ind[ind_2_sorted[:num_remember]]]) / float(num_remember)

    # 4. 挑选小损失样本的索引
    ind_1_update = ind_1_sorted[:num_remember]  # 网络1选出的样本索引
    ind_2_update = ind_2_sorted[:num_remember]  # 网络2选出的样本索引

    # 5. 交叉更新 (Co-teaching 核心)
    # 网络1使用网络2选出的样本来更新参数
    loss_1_update = F.cross_entropy(y_1[ind_2_update], t[ind_2_update])
    # 网络2使用网络1选出的样本来更新参数
    loss_2_update = F.cross_entropy(y_2[ind_1_update], t[ind_1_update])

    # 6. 返回平均损失以及保留样本的纯净比例
    return torch.sum(loss_1_update)/num_remember, torch.sum(loss_2_update)/num_remember, pure_ratio_1, pure_ratio_2

Curriculum Learning

课程学习借鉴了人类和动物的学习方式：按由易到难的顺序呈现训练样例，而非随机呈现。这种策略有助于机器学习算法更快收敛，并在非凸优化问题中找到更优的局部最小值。

核心动机：

• 学习更复杂的概念之前先掌握简单概念

• 避免学习器被噪声或过难的样例干扰

• 引导优化过程进入更好的参数空间区域

课程学习与深度学习优化问题

• 深度神经网络训练是一个高度非凸的优化问题，随机初始化往往难以找到优质解

• 课程学习可视为一种特殊的 continuation 方法（continuation method）：

  • 先优化“易”的目标（如噪声小、简单样例）

  • 再逐步过渡到“难”的目标（复杂样例或最终训练集）

• 类似于深度网络中的无监督预训练（Erhan et al., 2009），有助于优化和正则化

最小熵正则化（Minimum Entropy Regularization, MER）

相关论文:

1. Grandvalet, Yves and Bengio, Yoshua. Semi-supervised learning by entropy minimization. In Advances in Neural Information Processing Systems, pp. 529–536, 2005

2. Grandvalet, Yves and Bengio, Yoshua. 9 entropy regularization. 2006

在半监督学习中，我们通常有：

• 少量带标签数据（labeled data）

• 大量未标注数据（unlabeled data）

传统的监督学习只能利用带标签数据，忽略了未标注部分。但实际上，未标注数据蕴含着输入分布的重要信息（比如样本的聚类结构），如果能把它们利用起来，就能让分类器泛化得更好。

MER 的动机就是：希望分类器在未标注样本上也给出“明确的、高置信度”的预测，而不是模棱两可。

方法思想

分类器的输出一般是一个概率分布 $p(y|x)$，其中 $y$ 是类别，$x$ 是输入。

• 如果预测分布很接近均匀分布（例如 $[0.33,0.34,0.33]$），说明模型在样本 $x$ 上“不确定”。

• 如果预测分布很“尖锐”（例如 $[0.98,0.01,0.01]$），说明模型“有把握”。

MER 就是通过最小化 熵（entropy） 来鼓励分类器在未标注样本上的预测尽可能尖锐。

具体来说：

• 带标签样本：正常使用交叉熵损失。

• 未标注样本：在损失中额外加上预测分布的熵：

  $$L_u=\sum _{x\in U}H(p(y|x))=-\sum _{x\in U}\sum _{c}p(y=c|x)\log p(y=c|x)$$

然后最小化这个熵（即让预测分布更“确定”）。

最终的目标函数是：

$$L=L_{sup}+\lambda L_u$$

其中 $L_{sup}$ 是有监督的交叉熵损失，$\lambda$ 控制未标注样本的一致性约束强度。

直观理解

• MER 的假设是 类簇假设（cluster assumption）：数据会自然分布在若干簇中，而决策边界应该落在样本密度较低的地方。

• 最小化未标注样本的熵，就相当于强迫分类器把未标注样本“推”向某个类别，从而使决策边界更符合簇结构。

优点

• 无需生成模型：不同于很多早期半监督方法（如基于 EM 的生成模型），MER 不要求建模输入的联合分布 $p(x,y)$，只需优化判别模型即可。

• 适合高维数据：例如图像、语音，构建生成模型困难，而 MER 只需在分类器的输出空间加约束。

• 易于实现：只是在损失函数中额外加一个熵正则项。

与后续方法的联系

• Pseudo-Labeling（伪标签法）（Lee, 2013）：可以看作 MER 的“硬版本”，直接把未标注样本的预测结果当作伪标签再训练。

• Consistency Regularization（如 Π-model, Mean Teacher）：强调模型在未标注样本的不同扰动下保持一致，本质上也是让预测更稳定、置信度更高。

最小熵正则化通过在未标注样本上最小化预测分布的熵，鼓励分类器给出明确的预测，从而利用未标注数据的结构信息来提升性能。

Training Deep Neural Networks on Noisy Labels with Bootstrapping

在多类别分类任务中，训练数据可能存在噪声或缺失标签：

• 标签可能被标错（noisy labels）

• 部分样本缺失标签（missing labels）

• 传统 softmax 分类只最小化交叉熵 $-\sum _k{t}_k\log q_k$，无法处理噪声或不完整标签

目标：设计一种方法，使模型预测在面对噪声和缺失标签时仍保持 感知一致性（perceptual consistency），即相似输入得到相似预测。

自举（Bootstrapping）方法核心思想

自举方法通过 动态更新训练目标 来实现一致性：

1. 基本思想：

   • 不完全信任训练标签 $t$

   • 将训练目标调整为 训练标签与模型当前预测的凸组合

2. 公式表示：

• Soft 自举（Soft Bootstrapping）：直接使用模型预测概率 $q_k$

$$L_{\text{soft}}(q,t)=-\sum _k[\beta t_k+(1-\beta )q_k]\log q_k$$

• Hard 自举（Hard Bootstrapping）：使用模型预测的最大概率类别（MAP estimate）

$$z_k=1[k=\arg \underset{i}{max}{q}_i],L_{\text{hard}}(q,t)=-\sum _k[\beta t_k+(1-\beta )z_k]\log q_k$$

其中 $\beta \in [0,1]$ 控制对原标签的信任度：

• β 越大 → 越依赖原标签

• β 越小 → 越依赖模型自身预测

算法直观理解

• 类似 EM-like：

  1. E 步：根据当前模型输出，生成新的训练目标

  2. M 步：优化模型参数，使输出更接近生成的目标

• 随着训练进行：

  • 模型对错误标签的影响越来越小

  • 对一致性高的预测越来越自信

  • 模型在训练中逐渐修正噪声标签，实现自我增强（self-bootstrapping）

Robust early-learning: Hindering the memorization of noisy labels

彩票假设: The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks

在深度学习中，噪声标签（noisy labels） 是一个常见且严重的问题：

• 大规模数据集往往由人工或爬虫生成，容易出现错误标注。

• 深度神经网络有强大的拟合能力，会先学到干净标签的模式，但随后也会开始记住噪声标签（即“记忆效应”）。

• 这会导致模型过拟合噪声数据，泛化性能下降。

现有方法主要通过 修改损失函数、构造噪声转移矩阵、元学习、双网络训练等手段来缓解噪声问题，但这些方法复杂，且未充分利用参数层面的结构信息。

因此，论文要解决的问题是：如何在深度网络训练过程中，识别并抑制容易拟合噪声的参数，同时保留对干净标签有贡献的参数，从而提升模型鲁棒性。

核心思想

借鉴“彩票假设（lottery ticket hypothesis）”，区分网络中“关键参数（critical parameters）”和“非关键参数（non-critical parameters）”，并在训练时采用不同的更新策略，以减弱噪声标签的干扰。

展开来说：

1. 参数重要性判别

   • 通过新定义的最优性判据（$G^{\prime }(1)=⟨\mathrm{\nabla }L(W;S),W⟩$），衡量每个参数 $w_i$ 的贡献：

     $g_i=|\mathrm{\nabla }L(w_i;S)\cdot w_i|$

   • $g_i$ 大 → 参数对拟合干净标签重要（关键参数）。

   • $g_i$ 小 → 容易去拟合噪声（非关键参数）。

2. 参数划分与噪声率结合

   • 根据估计的噪声率 $\tau$，保留 $(1-\tau )m$ 个关键参数，其余视为非关键参数。

   • 直观理解：噪声率越高，需要依赖的关键参数越少。

3. 差异化更新规则

   • 关键参数 $W_c$： 使用损失函数梯度更新，但对梯度缩放 $(1-\tau )$，以避免过拟合噪声。

   • 非关键参数 $W_n$： 不使用梯度，只进行权重衰减，让其逐渐归零，防止学习噪声。

4. 最终效果

   • 模型只让关键参数主导学习过程，强化对干净标签的记忆。

   • 非关键参数被抑制，从而减少噪声标签的影响。

总结:

提出了一种参数级别的鲁棒早期学习方法（CDR, Combating noisy labels with Different update Rules），通过“关键参数保留 + 非关键参数衰减”的双更新机制，实现对带噪声标签数据的鲁棒训练。