1.TinyPytorch 第二阶段: 自动反向传播与框架基础能力提升
仓库链接: https://github.com/BinaryOracle/TinyPytorch
本节代码:
引言:从自动微分迈向通用框架
深度学习框架之所以强大,不仅因为其前向计算功能,更因为其背后复杂而精妙的自动微分系统。本系列文章试图揭开这些机制背后的本质,帮助读者从零搭建属于自己的深度学习引擎。
第一阶段中,我们构建了变量(Variable)与函数(Function)类,实现了基础的计算图结构与反向传播流程,并通过链式法则自动推导了导数。
第二阶段将从第11步延续,全面扩展 TinyPytorch 的核心能力。在第一阶段,我们完成了计算图与手动反向传播的雏形。而在本阶段,我们将继续揭开深度学习框架的核心机制:实现真正意义上的自动反向传播、多输入/输出处理、计算图遍历优化、梯度累加、配置控制等。通过这 14 个步骤,TinyPytorch 将蜕变为一个更通用、更高效、更接近真实框架的自动微分系统。
步骤11: 多输入与多输出
现实中的神经网络操作往往不仅仅接受一个输入,也可能产生多个输出,例如加法、乘法、切片、拼接等操作。因此我们扩展 Function 类以支持 可变参数输入与输出列表。
class Function:
def __call__(self, *inputs):
xs = [x.data for x in inputs]
ys = self.forward(*xs)
if not isinstance(ys, tuple):
ys = (ys,)
outputs = [Variable(as_array(y)) for y in ys]
for output in outputs:
output.set_creator(self)
self.inputs = inputs
self.outputs = outputs
return outputs if len(outputs) > 1 else outputs[0]
def forward(self, xs):
raise NotImplementedError()
def backward(self, gys):
raise NotImplementedError()这一扩展使我们的函数定义更接近 NumPy 风格,支持多个输入与输出,提高了灵活性。

为了更好地支持多输入函数,我们学习和利用了 Python 中的几个语法技巧:
*args:接收任意个数的位置参数,用于函数的输入接口;
*xs解包语法:在调用如forward(*xs)时展开变量列表;
tuple判断:让返回值始终封装为元组,统一处理逻辑。
步骤12: backward 的多输入实现
在 Variable.backward() 中支持多输出节点:
class Variable:
...
def backward(self):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = [self.creator]
while funcs:
f = funcs.pop()
gys = [output.grad for output in f.outputs]
gxs = f.backward(*gys)
if not isinstance(gxs,tuple):
gxs = (gxs,)
for x, gx in zip(f.inputs, gxs):
x.grad = gx
if x.creator is not None:
funcs.append(x.creator)这里 gxs 和 f.inputs 的每个元素都是一一对应的。准确来说, 如果有第i个元素, 那么f.input[i]的导数值对应于gxs[i]。于是代码中使用zip 函数和 for 循环来设置每一对的导数。以上就是Variable类的新 backward 方法。

步骤13: 重置导数
当我们使用同一个变量分别进行多次计算时,我们希望每次计算都能得到正确的导数。为了实现这一点,我们需要在每次计算之前将导数重置为0。
下面为 Variable 类提供一个新的方法,实现变量导数的重置。
class Variable:
...
def cleargrad(self):
self.grad = None步骤14: 共享变量与梯度累加
当某个变量被多次用作输入时(例如 z = x + x),反向传播过程中它的梯度应累加。
这是因为同一个变量对输出的影响路径有多条。如果我们不进行累加,而是直接覆盖梯度值,就会导致只有最后一条路径上的梯度被保留,其他路径上的梯度信息将丢失。
例如:
x = Variable(np.array(3.0))
y = add(x, x) # x 被用作两次输入在反向传播过程中,x 的梯度来自两个路径:一条是第一个 x 到 y,另一条是第二个 x 到 y。如果我们不对这两个梯度求和,只保留一个,那么 x 的真实导数就会被低估一半,最终影响训练结果。
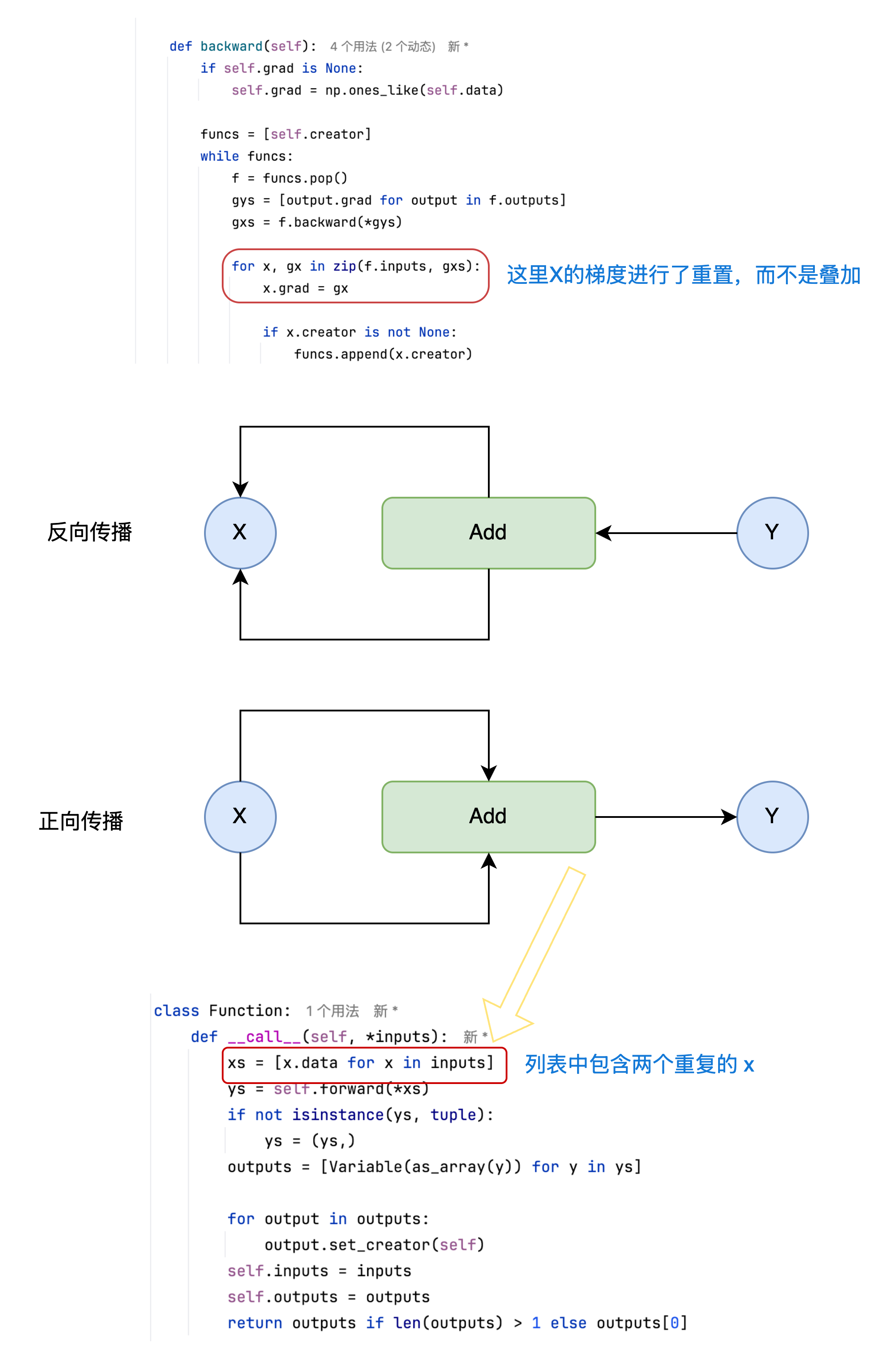
因此,在实现中应当如下处理:
class Variable:
...
def backward(self):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = [self.creator]
while funcs:
f = funcs.pop()
gys = [output.grad for output in f.outputs]
gxs = f.backward(*gys)
if not isinstance(gxs,tuple):
gxs = (gxs,)
for x, gx in zip(f.inputs, gxs):
if x.grad is None:
x.grad = gx
else:
x.grad = x.grad + gx # 正确的累加方式
if x.creator is not None:
funcs.append(x.creator)这样才能确保所有路径的贡献都被纳入最终的梯度值。
步骤15: 梯度重复累加的问题
在步骤14中,我们通过变量梯度非空则进行累加的改动,解决了共享变量梯度重置的问题,但是这一改动也引发了另一个问题:梯度重复累加。 观察下图,由于目前Variable.backward()的实现逻辑总是将函数追加到待处理列表的末尾,同时又优先处理列表末尾的函数,为"先进先出"的实现逻辑,因此对于存在多分支的复杂计算图而言,它也总是会沿着某个分支进行DFS直到"叶节点",这会导致如下图所示的共享变量a的梯度被重复累加,导致x变量梯度计算错误。
例子如下:
x = Variable(np.array(2.0))
a = square(x)
b = square(a)
c = square(a)
y = add(b, c)
y.backward()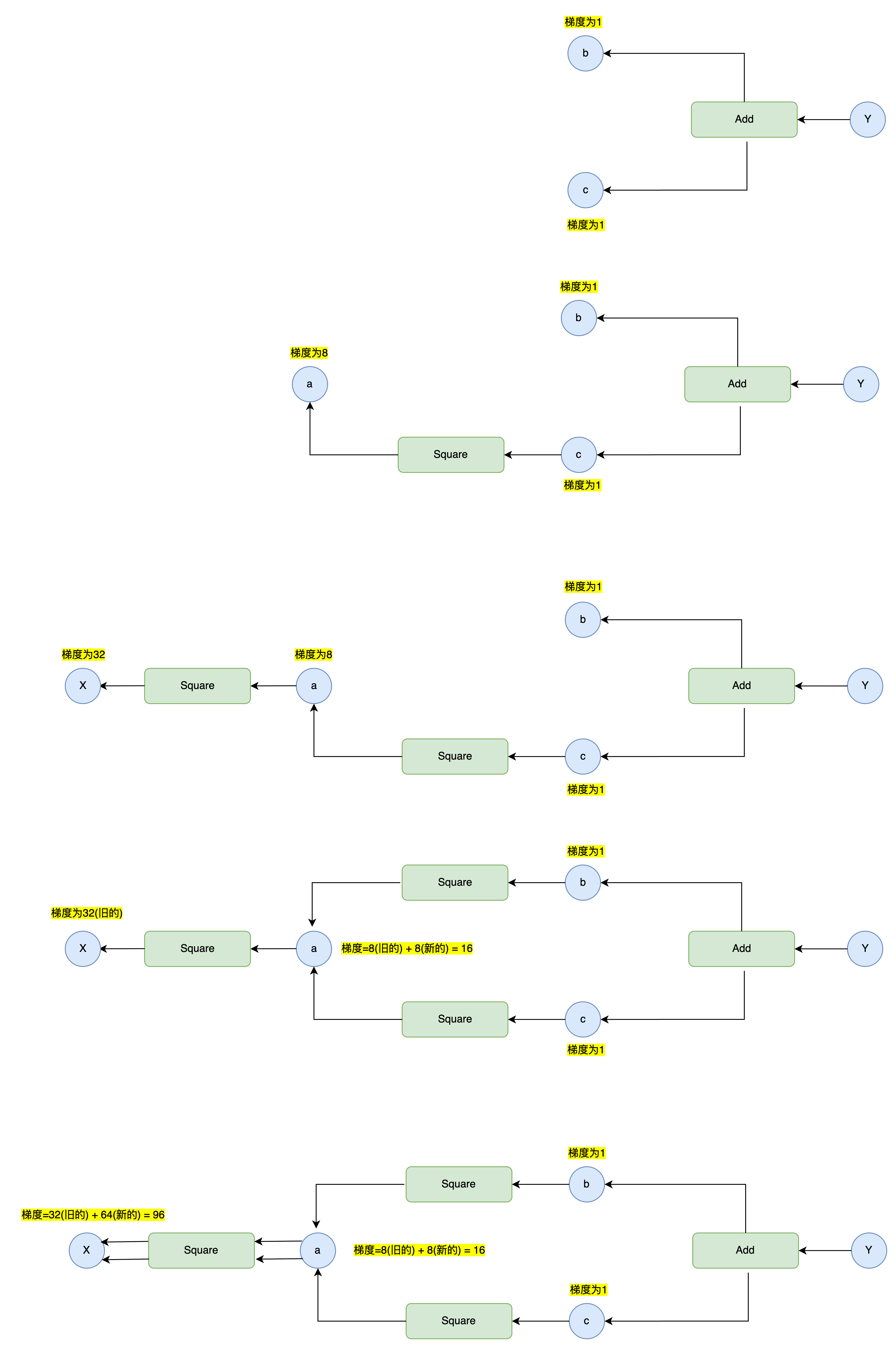
上面的问题本质是因为函数调用顺序错误导致的,对于共享变量,我们要先计算出其梯度后,才能继续计算其前向的梯度,其实也就是按照拓扑排序的方式去遍历计算图。
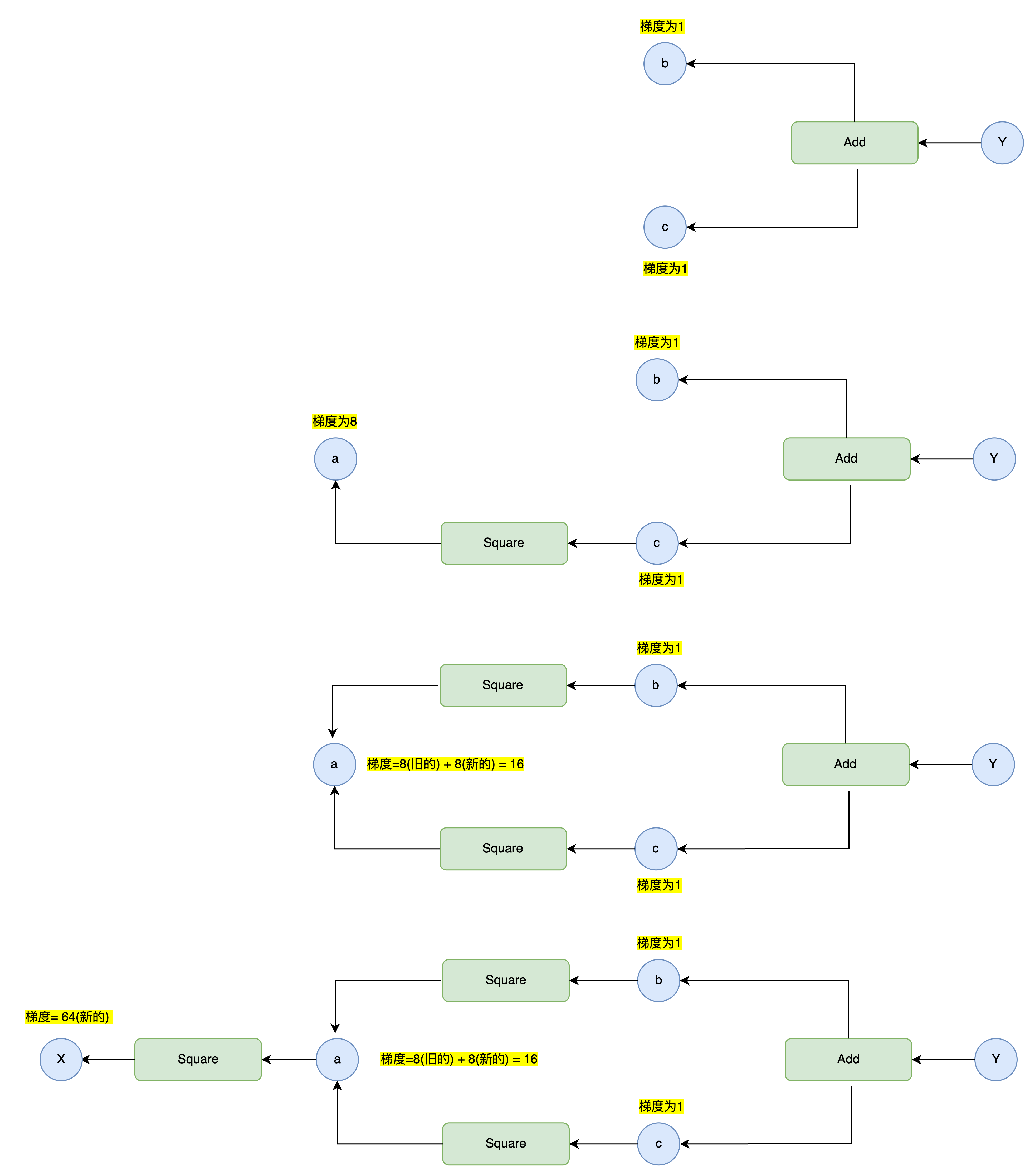
步骤16: "辈分"机制
为了解决上述的问题,我们可以采用拓扑排序,但是这里为了方便理解,我们采用更加暴力的“辈分排序”机制确保函数调用顺序的正确执行。
我们可以获取到哪个函数生成了哪个变量,这就构成了函数与变量的"辈分"关系;我们可以通过变量的辈分来设置其创建者函数的辈分,如下图所示:
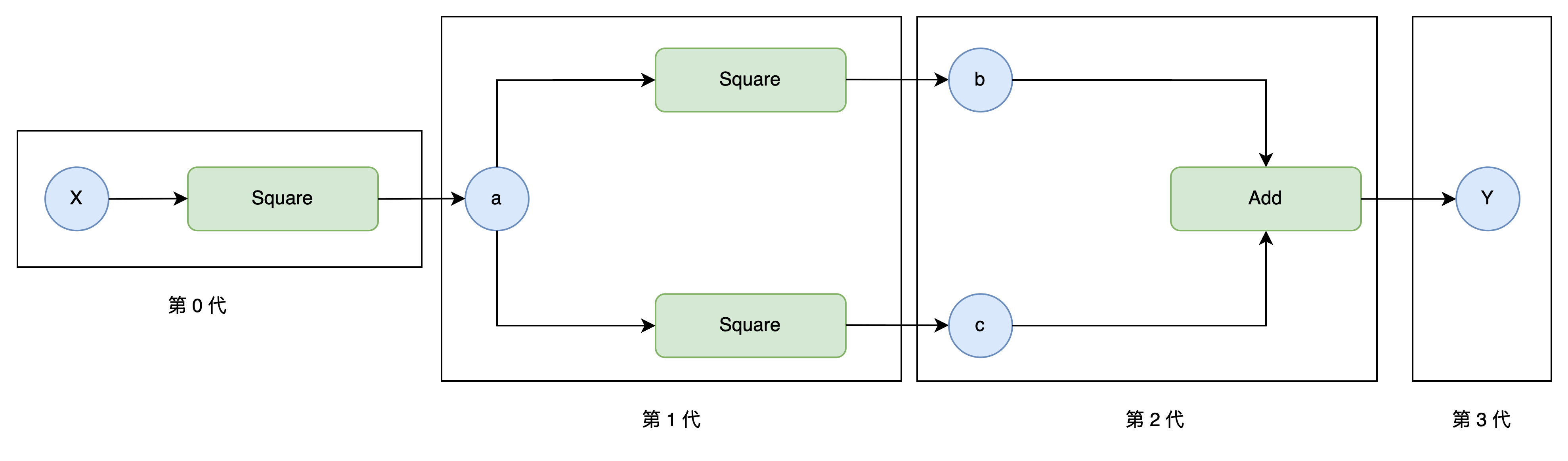
我们在Variable类和Function类中增加实例变量generation,用其来表示函数(或变量)属于哪一代。
class Variable:
def __init__ (self , data):
if data is not None:
if not isinstance(data , np.ndarray):
raise TypeError( '{} is not supported' .format(type(data)))
self.data = data
self.grad = None
self.creator = None
self.generation = 0
def set_creator(self, func):
self.creator = func
self.generation = func.generation + 1
...Variable 类将 generation 初始化为 0。之后, 当 set_creator 方法被调用时, 它将 generation 的值设置为父函数的 generation 值加1。
Function 类的 generation 被设置为多个输入变量中最大的generation的值。
class Function:
def __call__(self, *inputs):
xs = [x.data for x in inputs]
ys = self.forward(*xs)
if not isinstance(ys, tuple):
ys = (ys,)
outputs = [Variable(as_array(y)) for y in ys]
self.generation = max([x.generation for x in inputs])
for output in outputs:
output.set_creator(self)
self.inputs = inputs
self.outputs = outputs
return outputs if len(outputs) > 1 else outputs[0]通过以上修改, 在进行普通计算(即正向传播)时, 变量和函数中会设置好 generation 的值,我们便可以通过"辈分"按序取出元素。
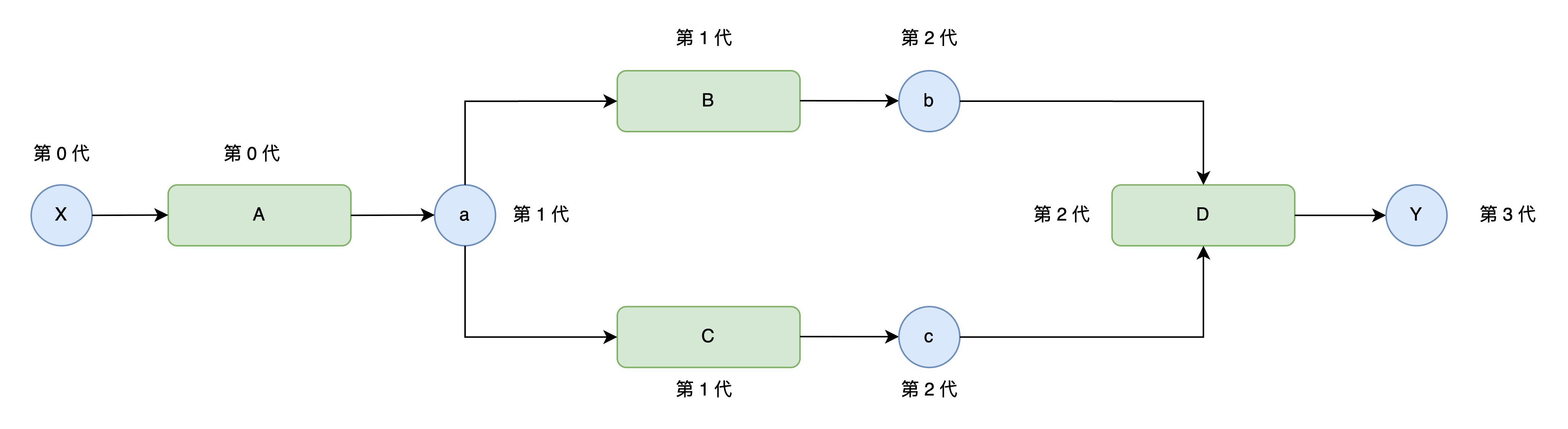
如上图所示,此时我们可以通过辈分来确保函数B和C先于函数A取出;我们只需要如下修改Variable变量的backward方法即可完成按照辈分获取函数的逻辑:
class Variable:
...
def backward(self):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = []
seen_set = set() # 防止同一个函数被多次添加到func列表中,从而避免一个函数的backward方法被错误地多次调用
def add_func(f):
if f not in seen_set:
funcs.append(f)
seen_set.add(f)
funcs.sort(key=lambda x : x.generation)
add_func(self.creator)
while funcs:
f = funcs.pop() # 每次取出辈分最大的函数
gys = [output.grad for output in f.outputs]
gxs = f.backward(*gys)
if not isinstance(gxs,tuple):
gxs = (gxs,)
for x, gx in zip(f.inputs, gxs):
if x.grad is None:
x.grad = gx
else:
x.grad = x.grad + gx # 正确的累加方式
if x.creator is not None:
add_func(x.creator)步骤17: 循环引用与内存释放
Python的内存管理主要依靠两种机制:引用计数和分代垃圾回收(GC)。在深度学习框架中,合理的内存管理至关重要,尤其当处理大规模数据时,不当的内存管理可能导致内存泄漏或程序崩溃。
引用计数:Python通过跟踪对象的引用次数来管理内存。当对象的引用计数为0时,会被立即回收。以下情况会增加引用计数:
使用赋值运算符(如
a = obj())向函数传递参数(如
f(a))向容器对象(列表、元组等)添加元素。
循环引用指对象之间相互引用,导致引用计数无法归零,从而无法被自动回收。例如:
a = Obj()
b = Obj()
c = Obj()
a.b = b
b.c = c
c.a = a
a = b = c = None # 此时a、b、c的引用计数仍为1,无法回收这种情况下,尽管用户不再访问这些对象,但因循环引用,引用计数无法降至0,需依赖垃圾回收机制处理。
虽然Python的垃圾回收(GC)机制可以处理循环引用对象,但在对内存敏感的场景下依然存在问题,主要原因如下:
回收时机非即时性: GC是一种后台机制,通常在内存不足或满足特定条件时才会触发,而非实时回收循环引用对象。例如,当TinyPytorch处理大量神经网络计算时,若存在循环引用,GC可能无法及时释放内存,导致内存占用持续升高,甚至引发内存不足错误。
性能开销较高: GC需要扫描整个对象图来检测循环引用,这一过程对大规模计算框架(如TinyPytorch)而言可能产生显著的性能损耗。尤其在神经网络训练中,频繁的GC操作会影响计算效率,而弱引用可通过避免循环引用直接解决问题,减少GC触发频率。
TinyPytorch中的循环引用:
当前TinyPytorch框架中,Function和Variable实例存在循环引用:
Function实例引用输入和输出的Variable实例(self.inputs和self.outputs)。Variable实例通过creator属性引用创建它的Function实例。

解决方案:弱引用
弱引用的优势:
避免强引用导致的内存滞留:
Function和Variable之间原本存在强引用循环(Function引用Variable,Variable通过creator引用Function)。若使用强引用,即使计算图不再被用户访问,循环引用仍会导致对象无法释放。而弱引用不会增加对象的引用计数,当用户不再引用Variable时,对象可被立即回收,无需等待GC。符合框架设计需求: TinyPytorch的计算图需要动态构建和销毁,弱引用能确保计算图在使用完毕后自动释放内存。例如,当用户执行完一次前向传播和反向传播后,计算图中的中间变量(如
Function和临时Variable)应被及时回收,以释放内存供后续计算使用。
GC与弱引用的互补关系
GC作为兜底机制:GC可处理开发者未显式解决的循环引用,但无法替代弱引用在框架设计中的针对性优化。
弱引用作为主动优化:在TinyPytorch中,通过弱引用主动打破
Function与Variable之间的循环引用,能更精准地控制内存释放时机,避免因GC延迟导致的内存问题。
使用Python的weakref模块创建弱引用,避免增加对象的引用计数:
- 修改
Function类:
import weakref
class Function:
def __call__(self, *inputs):
# 原有代码...
self.outputs = [weakref.ref(output) for output in outputs] # 将强引用改为弱引用弱引用不会增加对象的引用计数,当Variable实例不再被其他对象引用时,会被正常回收。
- 修改
Variable类的backward方法:
class Variable:
def backward(self):
# 原有代码...
gys = [output().grad for output in f.outputs] # 通过output()获取实际对象使用output()从弱引用中获取Variable实例,避免直接引用导致循环。
总结:
循环引用会导致Python对象无法被正常回收,需通过弱引用解决。
在TinyPytorch中,将
Function对Variable的引用改为弱引用,避免内存泄漏。优化后的内存管理确保框架在处理大规模计算时的稳定性和效率。
步骤18: 优化内存消耗
优化反向传播的内存消耗: TinyPytorch当前的反向传播会保留所有变量的导数,但在实际应用中,仅终端变量的导数需要被保留,中间变量的导数往往无用。为此,我们引入释放中间变量导数的机制。
修改Variable.backward方法: 添加retain_grad参数,若为False(默认),则反向传播后清除中间变量的导数。
class Variable:
def backward(self, retain_grad=False):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = []
seen_set = set()
def add_func(f):
if f not in seen_set:
funcs.append(f)
seen_set.add(f)
funcs.sort(key=lambda x: x.generation)
add_func(self.creator)
while funcs:
f = funcs.pop()
gys = [output().grad for output in f.outputs]
gxs = f.backward(*gys)
if not isinstance(gxs, tuple):
gxs = (gxs,)
for x, gx in zip(f.inputs, gxs):
if x.grad is None:
x.grad = gx
else:
x.grad = x.grad + gx
if x.creator is not None:
add_func(x.creator)
if not retain_grad:
for y in f.outputs:
y().grad = None # 清除中间变量的导数- 验证案例:
x0 = Variable(np.array(1.0))
x1 = Variable(np.array(1.0))
t = add(x0, x1)
y = add(x0, t)
y.backward() # retain_grad默认False
print(y.grad, t.grad) # 输出:None None(中间变量导数被清除)
print(x0.grad, x1.grad) # 输出:2.0 1.0(终端变量导数保留)中间变量y和t的导数被立即释放,减少内存占用。
禁用反向传播的模式优化: 在推理阶段(如模型预测),无需计算导数,可通过禁用反向传播模式进一步节省内存。
- 创建配置类
Config:
class Config:
enable_backprop = True # 控制反向传播是否启用- 修改
Function.__call__方法: 仅当Config.enable_backprop为True时,保留反向传播所需的计算图连接:
class Function:
def __call__(self, *inputs):
xs = [x.data for x in inputs]
ys = self.forward(*xs)
if not isinstance(ys, tuple):
ys = (ys,)
outputs = [Variable(as_array(y)) for y in ys]
if Config.enable_backprop:
self.generation = max([x.generation for x in inputs])
for output in outputs:
output.set_creator(self)
self.inputs = inputs
self.outputs = [weakref.ref(output) for output in outputs]
return outputs if len(outputs) > 1 else outputs[0]- 模式切换示例:
# 启用反向传播(默认模式)
x = Variable(np.ones((100, 100, 100)))
y = square(square(square(x))) # 保留中间结果,内存占用高
# 禁用反向传播(推理模式)
Config.enable_backprop = False
x = Variable(np.ones((100, 100, 100)))
y = square(square(square(x))) # 不保留中间结果,内存占用低禁用模式下,计算完成后中间变量立即释放,内存使用量大幅降低。
使用with语句便捷切换模式: 为避免手动修改Config属性,可通过contextlib模块实现with语句上下文管理。
- 实现
using_config函数:
import contextlib
@contextlib.contextmanager
def using_config(name, value):
old_value = getattr(Config, name)
setattr(Config, name, value)
try:
yield
finally:
setattr(Config, name, old_value)- 封装
no_grad函数:
def no_grad():
return using_config('enable_backprop', False)
# 使用示例
with no_grad():
x = Variable(np.array(2.0))
y = square(x) # 禁用反向传播,不构建计算图退出with块后,模式自动恢复,避免因忘记重置配置导致的错误。
优化效果总结:
内存释放机制:通过
retain_grad参数及时清除中间变量导数,避免内存长期占用。推理模式优化:禁用反向传播后,计算过程不保留计算图连接,适合无需梯度的场景(如模型预测)。
工程实践:
with no_grad()语法简洁,便于在训练和推理阶段灵活切换,提升代码可读性和鲁棒性。
步骤19: Variable 功能增强
为了便于区分和调试,在Variable类中添加name属性,支持为变量设置自定义名称:
class Variable:
def __init__(self, data, name=None):
if data is not None:
if not isinstance(data, np.ndarray):
raise TypeError(f'{type(data)} is not supported')
self.data = data
self.name = name # 新增名称属性
self.creator = None
self.grad = None
self.generation = 0- 使用示例:
x = Variable(np.array(1.0), name='input_x')
y = Variable(np.array(2.0), name='input_y')变量名称可在计算图可视化等场景中显示,提升调试效率。
使Variable实例具备ndarray的行为特征,隐藏数据封装细节:
- 添加
shape、ndim、size、dtype属性:
class Variable:
@property
def shape(self):
return self.data.shape # 获取数据形状
@property
def ndim(self):
return self.data.ndim # 获取维度数
@property
def size(self):
return self.data.size # 获取元素总数
@property
def dtype(self):
return self.data.dtype # 获取数据类型- 示例验证:
x = Variable(np.array([[1, 2, 3], [4, 5, 6]]))
print(x.shape) # 输出:(2, 3)
print(x.ndim) # 输出:2
print(x.size) # 输出:6
print(x.dtype) # 输出:int64变量实例可直接访问ndarray的核心属性,使用户无需关心data属性。
- 实现
__len__方法:
class Variable:
def __len__(self):
return len(self.data) # 返回第1维度的元素数- 示例:
x = Variable(np.array([1, 2, 3, 4]))
print(len(x)) # 输出:4
y = Variable(np.array([[1, 2], [3, 4]]))
print(len(y)) # 输出:2- 自定义打印格式:
class Variable:
def __repr__(self):
if self.data is None:
return 'variable(None)'
data_str = str(self.data).replace('\n', '\n' + ' ' * 9)
return f'variable({data_str})'- 输出效果:
x = Variable(np.array([1, 2, 3]))
print(x) # 输出:variable([1 2 3])
y = Variable(np.array([[1, 2], [3, 4]]))
print(y) # 输出:
# variable([[1 2]
# [3 4]])打印时自动对齐多行数据,并标注“variable”前缀,便于识别变量类型。
可继续添加
ndarray的其他属性(如T转置、flat迭代器等),或实现__getitem__、__setitem__方法以支持数组索引,进一步强化变量的“透明箱子”特性。
步骤20–22: 运算符重载
乘法运算的实现与运算符重载:
在深度学习框架中,乘法运算是最基础的操作之一。为了让Variable实例支持自然的乘法表达式(如a * b),我们需要实现Mul类来处理正向传播和反向传播,并将其绑定到*运算符上。
正向传播:计算两个输入变量的乘积,即
y = x0 * x1。反向传播:根据导数公式,若
y = x0 * x1,则gy分别乘以x1和x0,传递给下游变量。
class Mul(Function):
def forward(self, x0, x1):
y = x0 * x1
return y
def backward(self, gy):
x0, x1 = self.inputs[0].data, self.inputs[1].data
return gy * x1, gy * x0 # 将梯度分别乘以x1和x0为了方便使用,我们将Mul类封装为Python函数mul,并通过Variable.__mul__和Variable.__rmul__绑定乘法运算符,使其支持左右操作数为Variable的情况。由于乘法满足交换律,__mul__和__rmul__可共用同一实现。
def mul(x0, x1):
x1 = as_array(x1)
return Mul()(x0, x1)
Variable.__mul__ = mul # 处理a * b
Variable.__rmul__ = mul # 处理b * a加法运算的运算符重载:
加法运算的Add类已在上文中实现,其反向传播逻辑为将上游梯度原封不动地传递给两个输入变量(因为Add类绑定到+运算符:
def add(x0, x1):
x1 = as_array(x1)
return Add()(x0, x1)
Variable.__add__ = add # 处理a + b
Variable.__radd__ = add # 处理b + a复合运算的验证:
通过组合加法和乘法运算符,我们可以验证框架是否支持复杂表达式的自动微分。例如,计算y = a * b + c并求导:
a = Variable(np.array(3.0))
b = Variable(np.array(2.0))
c = Variable(np.array(1.0))
y = a * b + c # 等价于 add(mul(a, b), c)
y.backward()
print(y.data) # 输出:7.0(3*2+1)
print(a.grad) # 输出:2.0(∂y/∂a = b)
print(b.grad) # 输出:3.0(∂y/∂b = a)
print(c.grad) # 输出:1.0(∂y/∂c = 1)此例中,反向传播正确计算了每个变量的梯度,证明运算符重载与自动微分机制的一致性。
(可选部分) 在Python中,运算符重载需要同时考虑左右运算符(如__add__和__radd__),这是由Python的运算符调度机制决定的。当表达式中的左右操作数类型不同时,Python会根据操作数的类型选择不同的方法调用路径。Python中,运算符的调用顺序遵循以下规则:
左操作数优先:当执行表达式
a OP b时,Python首先尝试调用左操作数a的__OP__方法。右操作数 fallback:如果左操作数未实现
__OP__方法,或返回NotImplemented,则尝试调用右操作数b的__rOP__方法。
以加法a + b为例:
首先调用
a.__add__(b);若
a未实现__add__或返回NotImplemented,则调用b.__radd__(a)。
当操作数类型不同时(如Variable与数值、ndarray混合运算),必须通过__rOP__处理右操作数为自定义类型的情况。例如:
x + 3:左操作数x是Variable,调用x.__add__(3),可正常转换3为Variable;3 + x:左操作数3是int,不具备__add__方法处理Variable,因此需调用x.__radd__(3)。
在Python的运算符重载中,以def __add__(self, other)为例,self和other是两个关键入参:
self:在表达式a + b中,self指代左操作数a,即调用__add__方法的实例。other:在表达式a + b中,other指代右操作数b,即调用__radd__方法的实例。
在 Python 的运算符重载中,以def radd(self, other)为例,self和other是两个关键入参:
在表达式
a + b中,若左操作数a不支持__add__方法(或返回NotImplemented),则会调用右操作数b的__radd__方法。此时,self指代右操作数b,即调用__radd__方法的实例在
__radd__方法中,other指代左操作数a,其类型可能是原生数值、ndarray或Variable。
支持与ndarray及数值类型的混合运算:
为了提升框架的易用性,我们需要让Variable实例能与NumPy数组(ndarray)、Python数值类型(如int、float)直接进行运算。关键在于实现类型转换工具函数as_variable,将非Variable对象转换为Variable实例:
def as_variable(obj):
if isinstance(obj, Variable):
return obj
return Variable(obj) # 将ndarray或数值转换为Variable同时,修改Function类的__call__方法,在接收输入时自动将参数转换为Variable:
class Function:
def __call__(self, *inputs):
inputs = [as_variable(x) for x in inputs] # 统一转换为Variable
xs = [x.data for x in inputs]
# 后续计算逻辑...并且在所有重载运算符函数实现中,将other参数统一转换为ndarray:
def add(self, other):
other = as_array(other)
return Add()(self, other)
def as_array(x):
if np.isscalar(x):
return np.array(x)
return x这样,当执行x + np.array(3.0)或x + 3.0时,右侧的ndarray或数值会被自动转换为Variable,确保运算正常进行。
处理运算符的左右操作数差异:
以乘法为例,当表达式为3.0 * x时,Python会调用x的__rmul__方法(右乘)。由于乘法满足交换律,__rmul__可复用__mul__的实现:
Variable.__rmul__ = mul # 与__mul__共用逻辑,支持3.0 * x类似地,对于不满足交换律的运算符(如减法),需要分别处理左右操作数。例如,2.0 - x需要调用x的__rsub__方法,此时需交换操作数顺序并调用Sub类:
def rsub(x0, x1):
return Sub()(x1, x0) # 实现a - b = Sub(b, a)
Variable.__rsub__ = rsub运算符优先级与类型转换:
为了确保Variable实例在混合运算中优先被处理,我们为Variable类添加__array_priority__属性,设置其优先级高于ndarray(默认优先级为100):
class Variable:
__array_priority__ = 200 # 高于ndarray的优先级,确保类型转换优先这使得当表达式为np.array([2.0]) + x时,x的__radd__方法会被优先调用,保证运算按预期执行。
负数运算(-)的实现:
负数运算y = -x的正向传播简单地对输入取反,反向传播时将上游梯度取反(因为
class Neg(Function):
def forward(self, x):
return -x
def backward(self, gy):
return -gy # 梯度取反绑定-运算符到neg函数:
def neg(x):
return Neg()(x)
Variable.__neg__ = neg # 支持y = -x减法运算(-)的完整实现:
减法运算y = x0 - x1的反向传播中,gy分别乘以1和-1:
class Sub(Function):
def forward(self, x0, x1):
return x0 - x1
def backward(self, gy):
return gy, -gy # 梯度分别乘以1和-1由于减法不满足交换律,需分别实现__sub__(处理x0 - x1)和__rsub__(处理x1 - x0):
def sub(x0, x1):
return Sub()(x0, x1)
def rsub(x0, x1):
return Sub()(x1, x0) # 交换操作数实现a - b
Variable.__sub__ = sub # 支持x0 - x1
Variable.__rsub__ = rsub # 支持x1 - x0除法运算(/)的实现:
除法运算y = x0 / x1的导数公式为
class Div(Function):
def forward(self, x0, x1):
return x0 / x1
def backward(self, gy):
x0, x1 = self.inputs[0].data, self.inputs[1].data
gx0 = gy / x1
gx1 = -gy * x0 / (x1 ** 2)
return gx0, gx1 # 按导数公式计算梯度同样,需处理左右操作数的除法运算:
def div(x0, x1):
return Div()(x0, x1)
def rdiv(x0, x1):
return Div()(x1, x0) # 交换操作数实现a / b
Variable.__truediv__ = div # 支持x0 / x1
Variable.__rtruediv__ = rdiv # 支持x1 / x0幂运算(**)的实现:
幂运算y = x ** c中,c为常数指数,其导数公式为
class Pow(Function):
def __init__(self, c):
self.c = c # 保存指数
def forward(self, x):
return x ** self.c
def backward(self, gy):
x = self.inputs[0].data
c = self.c
gx = c * (x ** (c - 1)) * gy # 导数公式:c·x^(c-1)·gy
return gx绑定**运算符到pow函数:
def pow(x, c):
return Pow(c)(x)
Variable.__pow__ = pow # 支持x ** c通过步骤20-22的实现,TinyPytorch框架实现了完整的运算符重载体系,使开发者能以自然的数学表达式编写代码(如y = (x + 3) ** 2 / 2),而无需调用特定函数。这种“可微分编程”的方式不仅降低了学习成本,还确保了复杂表达式的自动微分正确性,为后续实现神经网络层和优化算法奠定了基础。
步骤23: 项目模块化结构
在Python开发中,模块、包和库是组织代码的重要方式:
模块(module):单个Python文件,如
core.py,用于封装功能。包(package):多个模块的集合,以目录形式存在,需包含
__init__.py文件。库(library):多个包的集合,通常用于实现完整功能(如TinyPytorch框架)。
为将 TinyPytorch 的代码组织为可复用的包,从本章开始为每个Chapter设计如下目录结构:
__init__.py # 包初始化文件
core.py # 核心功能(简化版)
functions.py # 具体函数实现
utils.py # 工具函数core.py,包括:
类定义:
Config、Variable、Function及运算符相关类(Add、Mul等)。函数定义:
using_config、no_grad、as_array、as_variable等工具函数,以及add、mul等运算符函数。
__init__.py中导入核心类并初始化运算符重载:
from chapter2.core import Variable
from chapter2.core import Function
from chapter2.core import using_config
from chapter2.core import no_grad
from chapter2.core import as_array
from chapter2.core import as_variable
from chapter2.core import setup_variable
setup_variable() # 初始化运算符重载其中,setup_variable()函数负责绑定运算符方法:
def setup_variable():
Variable.__add__ = add
Variable.__radd__ = add
Variable.__mul__ = mul
Variable.__rmul__ = mul
# 其他运算符绑定...步骤24:复杂函数的求导
优化问题中常使用特定函数评估算法性能,这些函数被称为测试函数。通过对复杂测试函数求导,可验证TinyPytorch框架处理高阶微分的能力。本步骤选取3个经典测试函数,演示TinyPytorch的自动微分功能。
Sphere函数求导
函数定义:
代码实现:
def sphere(x, y): z = x ** 2 + y ** 2 return z x = Variable(np.array(1.0)) y = Variable(np.array(1.0)) z = sphere(x, y) z.backward() print(x.grad, y.grad) # 输出:2.0 2.0结果验证:根据导数公式
Matyas函数求导
函数定义:
代码实现:
def matyas(x, y): z = 0.26 * (x ** 2 + y ** 2) - 0.48 * x * y return z x = Variable(np.array(1.0)) y = Variable(np.array(1.0)) z = matyas(x, y) z.backward() print(x.grad, y.grad) # 输出:0.04 0.04(近似值)结果分析:通过运算符重载,可直接将数学表达式转译为代码。若不使用运算符,需编写繁琐的函数调用(如
sub(mul(0.26, add(pow(x, 2), pow(y, 2))), mul(0.48, mul(x, y))),凸显运算符重载的可读性优势。
Goldstein-Price函数求导
函数定义:
该函数形式复杂,包含高次项和交叉项,是验证框架能力的理想案例。
- 代码实现:
def goldstein(x, y): z = (1 + (x + y + 1)** 2 * (19 - 14*x + 3*x**2 - 14*y + 6*x*y + 3*y** 2)) * \ (30 + (2*x - 3*y)** 2 * (18 - 32*x + 12*x**2 + 48*y - 36*x*y + 27*y** 2)) return z x = Variable(np.array(1.0)) y = Variable(np.array(1.0)) z = goldstein(x, y) z.backward() print(x.grad, y.grad) # 输出:-5376.0 8064.0 - 结果验证:通过梯度检验可知结果正确。TinyPytorch框架能自动处理复杂表达式的微分,无需手动推导导数公式,体现了自动微分的优势。
TinyPytorch的核心能力总结
自然代码表达:支持将数学公式直接转译为Python代码,如
z = (x + y + 1)**2 * ...,无需额外接口。复杂计算图处理:无论计算图结构多复杂(如多层嵌套、高次运算),均能正确构建反向传播路径。
可微分编程:将普通数值计算转换为可微分计算,使深度学习框架具备自动求导能力,为优化算法和神经网络训练奠定基础。
深度学习框架的计算图范式: TinyPytorch采用Define-by-Run(动态计算图) 模式,与Define-and-Run(静态计算图)的对比如下:
Define-by-Run:计算与图构建同时进行,如TinyPytorch中每一步运算都会动态创建计算图链接,支持Python原生控制流(
if、while),调试便捷。Define-and-Run:先定义计算图再执行,需使用领域特定语言(如TensorFlow 1.x的tf.cond),适合大规模优化但灵活性较低。
TinyPytorch的动态计算图模式使其在易用性和灵活性上表现突出,尤其适合研究和快速开发场景。
第二阶段总结
这一阶段,我们构建了如下关键功能:
扩展DeZero以处理多输入多输出函数,支持用+、*等运算符自然表达计算。
修改Function类,通过列表处理可变长参数,优化正向传播实现。
实现多元函数反向传播,解决变量重复使用时的梯度累加问题。
引入“辈分”机制,确保复杂计算图反向传播顺序正确。
使用弱引用解决循环引用,通过Config类和no_grad模式优化内存管理。
重载运算符,支持Variable与数值、数组混合运算,提升代码可读性。
为Variable添加shape等属性,使其行为更接近NumPy数组,优化打印等交互体验。