🚀 从零构建深度学习框架（一）：计算图与自动微分的起点

1.TinyPytorch 第一阶段: 计算图与自动微分

仓库链接: https://github.com/BinaryOracle/TinyPytorch
本节代码:

引言：揭开深度学习框架的神秘面纱

深度学习框架中蕴藏着惊人的技术和有趣的机制，而本系列旨在揭开这些技术和机制的神秘面纱，帮助读者正确理解技术，体会它们的有趣之处。为此，本系列将带领读者从零开始创建一个深度学习框架——TinyPytorch。TinyPytorch尽量用最少的代码实现了现代深度学习框架的功能。第一阶段共包含10个步骤，让我们逐步构建起TinyPytorch的基础功能。

步骤1：作为"箱子"的变量

变量的基本概念

变量是TinyPytorch最重要的组成部分，可将其比作存放数据的"箱子"。在编程中，变量的作用是存储数据，而TinyPytorch的变量实现为Variable类，其核心功能是保存和管理数据。

代码实现

class Variable:
    def __init__(self, data):
        self.data = data

使用示例

import numpy as np

data = np.array(1.0)
x = Variable(data)
print(x.data)  # 输出 1.0

x.data = np.array(2.0)
print(x.data)  # 输出: 2.0

关键要点

• Variable类封装了NumPy的多维数组（ndarray）

• 数据存储在data属性中

• 支持数据的修改和读取

步骤2：创建变量的函数

函数与计算图

函数定义了变量之间的对应关系，通过计算图可以直观地表示变量与函数的关系。计算图用圆框表示变量，用方框表示函数，节点和箭头展示计算流程。

函数类的设计

设计Function类作为基类，具体函数继承该类并实现forward方法。__call__方法处理输入输出的变量封装。

代码实现

class Function:
    # 设定传入的input和返回的output均为Variable类型
    def __call__(self, input):
        x = input.data
        y = self.forward(x)
        output = Variable(y)
        return output
    
    def forward(self, x):
        raise NotImplementedError()

class Square(Function):
    def forward(self, x):
        return x ** 2

辅助函数

为了方便使用，将函数类封装为Python函数：

def square(x):
    return Square()(x)

步骤3：函数的连续调用

复合函数的计算

多个函数可以连续调用，形成复合函数。例如，计算$y=(e^{x^2}{)}^2$，可以通过连续使用平方函数和指数函数实现。

代码示例

class Exp(Function):
    def forward(self, x):
        return np.exp(x)

def exp(x):
    return Exp()(x)

A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
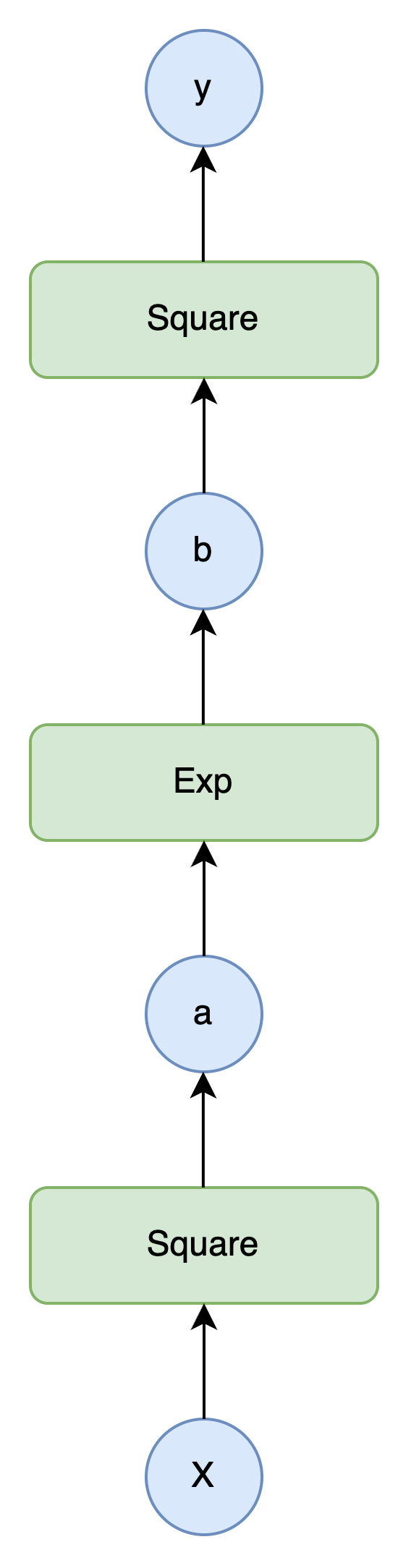
print(y.data)  # 输出: 1.648721270700128

计算图的意义

复合函数的计算图展示了函数的组合过程，而反向传播算法可以高效地求出每个变量的导数，这为自动微分奠定了基础。

步骤4：数值微分

导数的定义

导数是变化率的表示，函数$f(x)$在$x$处的导数定义为：

$$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f(x)}{h}$$

数值微分的实现

使用中心差分近似计算数值微分，公式为：

$$\frac{f(x+h)-f(x-h)}{2h}$$

本部分感兴趣的可以回顾高数中微分定义部分内容，中心差分近似可以问问GPT。

代码实现

def numerical_diff(f, x, eps=1e-4):
    x0 = Variable(x.data - eps)
    x1 = Variable(x.data + eps)
    y0 = f(x0)
    y1 = f(x1)
    return (y1.data - y0.data) / (2 * eps)

数值微分的问题

• 结果包含误差（精度丢失）

• 计算成本高（尤其对于多变量函数）

• 可用于梯度检验，验证反向传播的正确性

步骤5：反向传播的理论知识

链式法则

反向传播的理论基础是链式法则，对于复合函数$y=F(x)$，若$F$由$a=A(x)$、$b=B(a)$、$y=C(b)$组成，则：

$$\frac{dy}{dx}=\frac{dy}{db}\frac{db}{da}\frac{da}{dx}$$

反向传播的方向

反向传播按从输出到输入的顺序计算导数，与正向传播方向相反。这种方式在输出为标量的情况下计算效率更高，适合机器学习中损失函数的优化。

• 反向传播用于计算输入X对输出Y大小变化的影响，如果没有Function作用于X上，即Y=X，那么影响因子R恒为1；
  
  
• 如果存在Function作用在X上，那么Function可能会放大或者缩小X对输出Y大小变化的影响，也就是改变X对于Y的影响因子，此时R= 1 * F放缩因子；
  
  
• 如果存在多个Function先后作用在X上，即Y=Fn(...F2(F1(X)))，那么此时影响因子R= 1 * F1放缩因子 * F2放缩因子 * ... * Fn放缩因子；
  
  
• 对于Y=F2(F1(x)) + F3(x) , 此时影响因子R = 1 * F1放缩因子 * F2放缩因子 + 1 * F3放缩因子；
  
  
• 实际此处的函数放缩因子也称为函数的导数，多元场景下也称为偏导数。

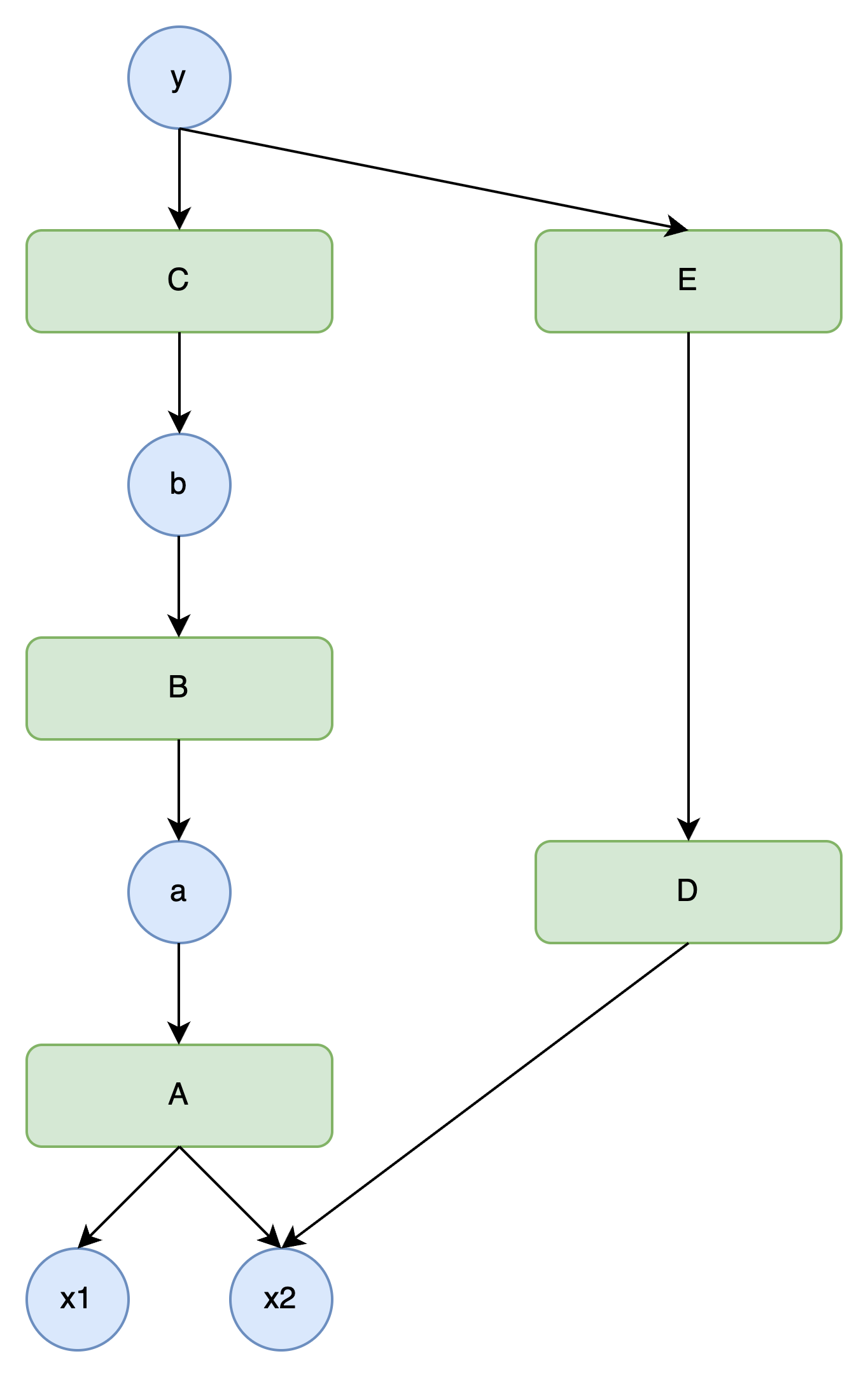
计算图的反向传播

反向传播过程中，导数从输出端向输入端传播，每个函数节点需要计算其导数，并将结果传递给前一层变量。

步骤6：手动进行反向传播

扩展Variable类

为Variable类添加grad属性，用于存储导数：

class Variable:
    def __init__(self, data):
        self.data = data
        self.grad = None

扩展Function类

为Function类添加反向传播方法backward，并在__call__方法中保存输入输出变量：

class Function:
    def __call__(self, input):
        x = input.data
        y = self.forward(x)
        output = Variable(y)
        self.input = input
        self.output = output
        return output
    
    def backward(self, gy):
        raise NotImplementedError()

反向传播的核心是依据链式法则，沿计算图反向推导各变量的导数。而链式法则的计算需要知晓每个函数在正向传播时的输入值。

例如，对于函数 $y=f(x)$ ，其导数 $\frac{dy}{dx}$ 依赖于输入x的具体值（如平方函数 $f(x)=x^2$ 的导数 $\frac{dy}{dx}=2x$ ，需要知道正向传播时的 $x$ 值）。记录input后，反向传播时可直接获取这些值，避免重复计算或存储额外数据。

具体函数的反向传播

以平方函数为例：

class Square(Function):
    def backward(self, gy):
        x = self.input.data
        gx = 2 * x * gy
        return gx

反向传播的执行

按反向顺序调用各函数的backward方法，手动传递导数：

y.grad = np.array(1.0)
b.grad = C.backward(y.grad)
a.grad = B.backward(b.grad)
x.grad = A.backward(a.grad)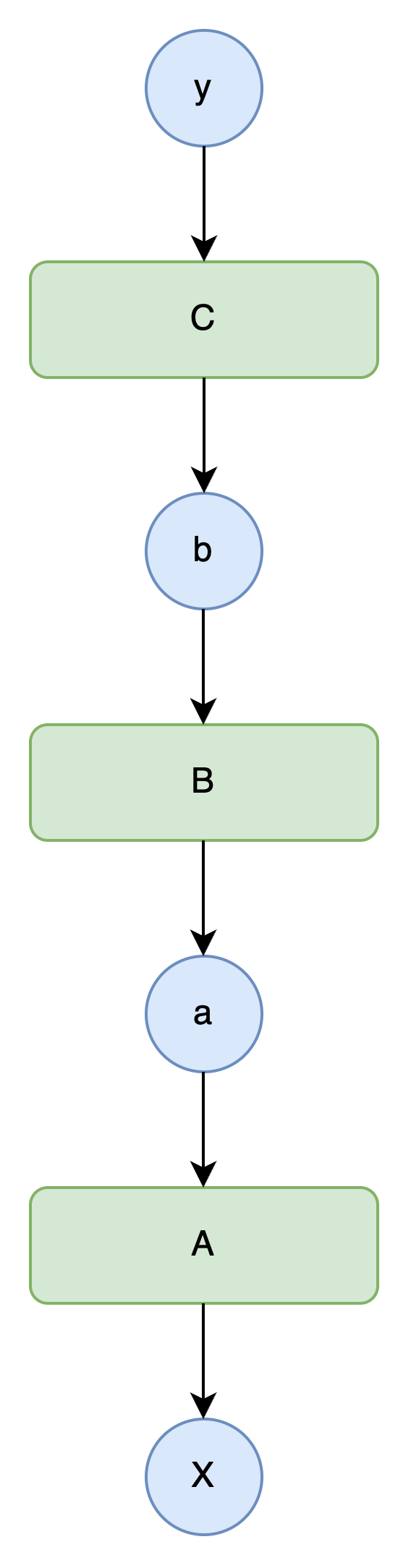

步骤7：反向传播的自动化

建立变量与函数的连接

在Variable类中添加creator属性，记录创建该变量的函数；在Function类的__call__方法中，设置变量的creator：

class Variable:
    def set_creator(self, func):
        self.creator = func

class Function:
    def __call__(self, input):
        # 其他代码...
        output.set_creator(self)

自动反向传播的实现

在Variable类中添加backward方法，通过递归或循环遍历计算图，自动执行反向传播：

class Variable:
    def backward(self):
        f = self.creator
        if f is not None:
            x = f.input
            x.grad = f.backward(self.grad)
            x.backward()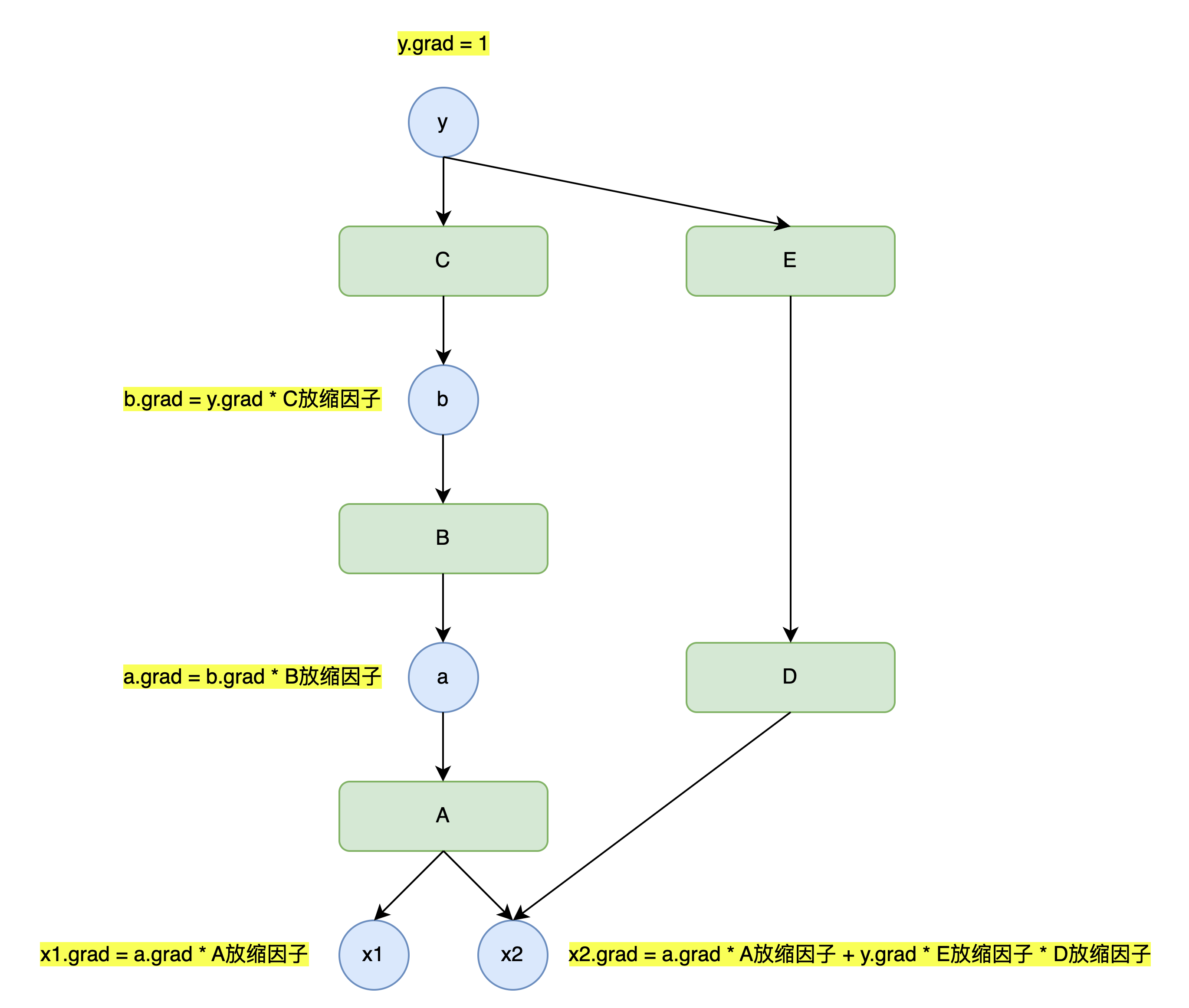

你品，你细品 ~ 🤔 (目前实现的版本无法实现上图中计算图多分支的结构，只能实现一条竖线形状的计算图结构的反向传播)

步骤8：从递归到循环

递归实现的问题

递归实现的反向传播在计算图较深时可能导致栈溢出，且效率较低。

循环实现反向传播

使用列表保存待处理的函数，通过循环替代递归：

class Variable:
    def backward(self):
        funcs = [self.creator]
        while funcs:
            f = funcs.pop() # 弹出列表尾部元素
            x, y = f.input, f.output
            x.grad = f.backward(y.grad)
            if x.creator is not None:
                funcs.append(x.creator) # 追加到列表尾部

由于目前只支持竖线形状的计算图，因此func列表同一时刻最多只存在一个func

循环实现的优势

• 避免栈溢出

• 提高执行效率

• 更容易处理复杂计算图

步骤9：让函数更易用

函数的Python化

将函数类封装为Python函数，便于直接调用：

def square(x):
    return Square()(x)

def exp(x):
    return Exp()(x)

自动设置梯度

在Variable的backward方法中自动初始化梯度：

class Variable:
    def backward(self):
        if self.grad is None:
            self.grad = np.ones_like(self.data)
        # 其他代码...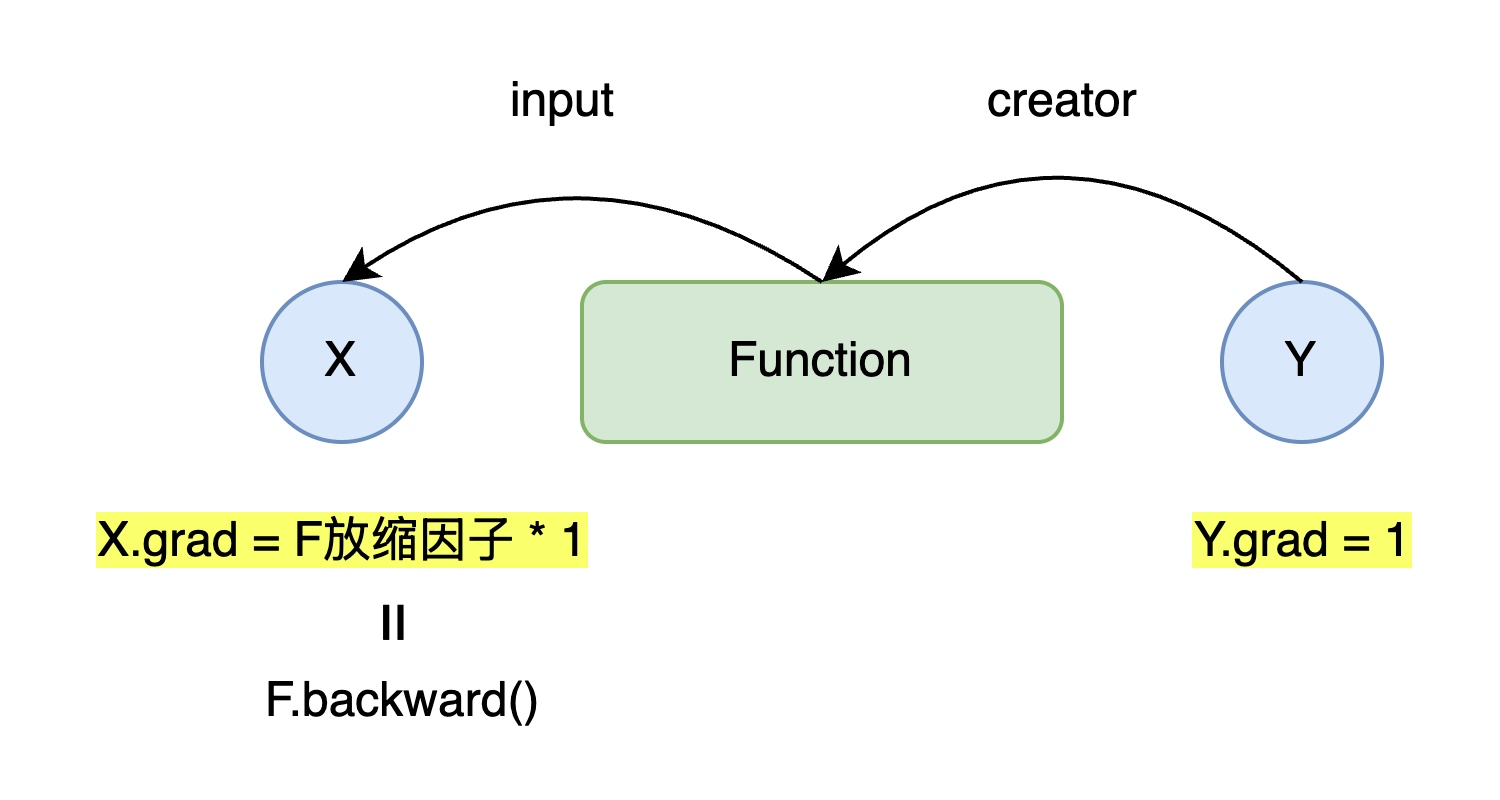

数据类型检查

确保Variable只接受ndarray实例，提高代码健壮性：

class Variable:
    def __init__(self, data):
        if data is not None:
            if not isinstance(data, np.ndarray):
                raise TypeError(f'{type(data)} is not supported')
        self.data = data
        # 其他代码...

步骤10：测试

单元测试

使用Python的unittest模块编写测试用例，验证函数的正向传播和反向传播：

import unittest

class SquareTest(unittest.TestCase):
    def test_forward(self):
        x = Variable(np.array(2.0))
        y = square(x)
        self.assertEqual(y.data, np.array(4.0))
    
    def test_backward(self):
        x = Variable(np.array(3.0))
        y = square(x)
        y.backward()
        self.assertEqual(x.grad, np.array(6.0))

梯度检验

将数值微分的结果与反向传播的结果进行比较，验证反向传播的正确性：

def numerical_diff(f, x, eps=1e-4):
    # 实现如前所述

class SquareTest(unittest.TestCase):
    def test_gradient_check(self):
        x = Variable(np.random.rand(1))
        y = square(x)
        y.backward()
        num_grad = numerical_diff(square, x)
        self.assertTrue(np.allclose(x.grad, num_grad))

测试的重要性

• 确保代码功能正确性

• 发现潜在bug

• 支持代码重构和扩展

第一阶段总结

通过第一阶段的10个步骤，我们从零开始构建了TinyPytorch框架的基础功能：

1. 实现了变量和函数的基本结构

2. 完成了自动微分的核心算法——反向传播

3. 实现了数值微分作为梯度检验工具

4. 优化了反向传播的实现，从递归改为循环

5. 提高了框架的易用性和健壮性

6. 建立了测试机制，确保代码质量

此时的TinyPytorch已经具备了自动微分的能力，可以处理简单的计算图，并为后续的功能扩展奠定了坚实基础。接下来的阶段将进一步扩展TinyPytorch，使其支持更复杂的计算和神经网络的构建。